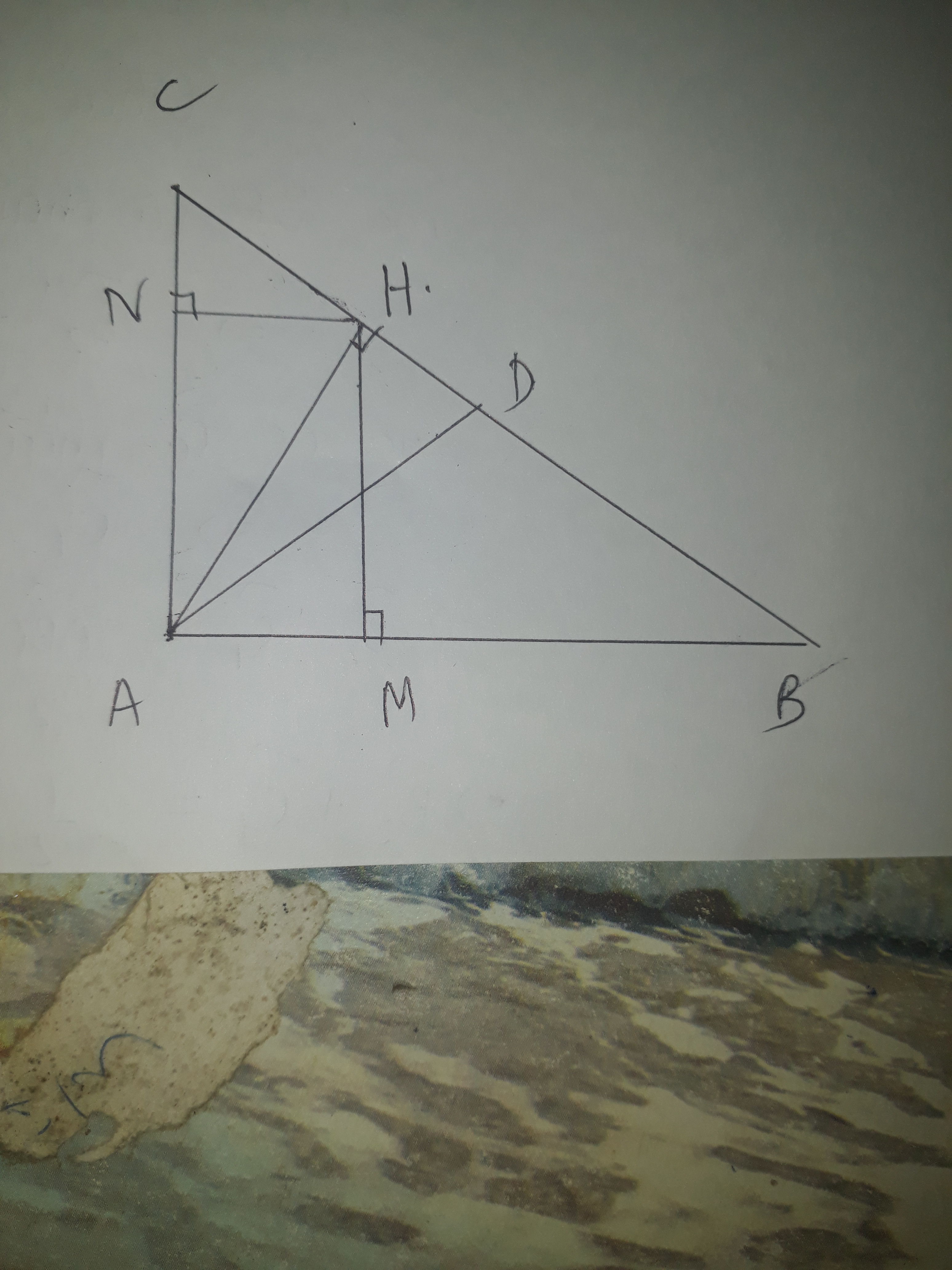
Tam giác ABC vuông tại A có AB=6 cm,Ac =4,5 cm
a)Giải tam giác ABC (góc làm tròn đến phút )
b)Gọi AH là đường cao, AD là trung tuyến .Tính Ad ,Ah và góc tạo Bởi AH và AD (Góc làm tròn đến phút )
c)Bỏ qua các số liệu cho trên .kẻ HM vuông góc với AB tại M,HN vuông góc với AC tại N. CM BM/CN =tan^3 C
mn giúp e phần C vs ạ
thanks trướC
Quảng cáo
2 câu trả lời 4150
Cho:
Tam giác ABCABCABC vuông tại A
AB=6AB = 6AB=6 cm
AC=4,5AC = 4{,}5AC=4,5 cm
a) Giải tam giác ABC
1️⃣ Tính cạnh huyền BCBCBC
BC=AB2+AC2=62+4,52=36+20,25=56,25=7,5 cmBC = \sqrt{AB^2 + AC^2} = \sqrt{6^2 + 4{,}5^2} = \sqrt{36 + 20{,}25} = \sqrt{56{,}25} = 7{,}5\ \text{cm}BC=AB2+AC2=62+4,52=36+20,25=56,25=7,5 cm
2️⃣ Tính các góc
Góc BBB:
sinB=ACBC=4,57,5=0,6\sin B = \frac{AC}{BC} = \frac{4{,}5}{7{,}5} = 0{,}6sinB=BCAC=7,54,5=0,6 B≈36,87∘≈36∘52′B \approx 36{,}87^\circ \approx 36^\circ52'B≈36,87∘≈36∘52′Góc CCC:
C=90∘−B≈53,13∘≈53∘08′C = 90^\circ - B \approx 53{,}13^\circ \approx 53^\circ08'C=90∘−B≈53,13∘≈53∘08′
✅ Kết quả câu a
BC=7,5BC = 7{,}5BC=7,5 cm
∠B≈36∘52′\angle B \approx 36^\circ52'∠B≈36∘52′
∠C≈53∘08′\angle C \approx 53^\circ08'∠C≈53∘08′
b) Tính ADADAD, AHAHAH và góc giữa AHAHAH và ADADAD
1️⃣ Tính ADADAD (trung tuyến ứng với cạnh huyền)
Trong tam giác vuông, trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền
AD=BC2=7,52=3,75 cmAD = \frac{BC}{2} = \frac{7{,}5}{2} = 3{,}75\ \text{cm}AD=2BC=27,5=3,75 cm
2️⃣ Tính AHAHAH (đường cao từ A xuống BC)
AH=AB⋅ACBC=6⋅4,57,5=277,5=3,6 cmAH = \frac{AB \cdot AC}{BC} = \frac{6 \cdot 4{,}5}{7{,}5} = \frac{27}{7{,}5} = 3{,}6\ \text{cm}AH=BCAB⋅AC=7,56⋅4,5=7,527=3,6 cm
3️⃣ Góc giữa AHAHAH và ADADAD
Đặt hệ trục tọa độ cho dễ tính:
A(0,0)A(0,0)A(0,0)
B(6,0)B(6,0)B(6,0)
C(0,4,5)C(0,4{,}5)C(0,4,5)
Tính được:
H(2,16; 1,62)H(2{,}16;\ 1{,}62)H(2,16; 1,62)
D(3; 2,25)D(3;\ 2{,}25)D(3; 2,25)
Vector:
AH⃗=(2,16; 1,62),AD⃗=(3; 2,25)\vec{AH} = (2{,}16;\ 1{,}62),\quad \vec{AD} = (3;\ 2{,}25)AH=(2,16; 1,62),AD=(3; 2,25)Áp dụng công thức tích vô hướng:
cosθ=AH⃗⋅AD⃗∣AH⃗∣∣AD⃗∣\cos \theta = \frac{\vec{AH}\cdot\vec{AD}}{|\vec{AH}||\vec{AD}|}cosθ=∣AH∣∣AD∣AH⋅ADTính ra:
θ≈0,13∘≈8′\theta \approx 0{,}13^\circ \approx 8'θ≈0,13∘≈8′
✅ Kết quả câu b
AD=3,75AD = 3{,}75AD=3,75 cm
AH=3,6AH = 3{,}6AH=3,6 cm
∠(AH,AD)≈0∘08′\angle (AH, AD) \approx 0^\circ08'∠(AH,AD)≈0∘08′
c) Chứng minh
Bỏ số liệu, dựng:
HM⊥ABHM \perp ABHM⊥AB tại MMM
HN⊥ACHN \perp ACHN⊥AC tại NNN
Cần chứng minh:
CM⋅BMCN=tan3C\frac{CM \cdot BM}{CN} = \tan^3 CCNCM⋅BM=tan3C✏️ Ý tưởng chứng minh (chuẩn hình học):
Từ các tam giác vuông nhỏ tạo bởi HM,HNHM, HNHM,HN, ta có:
BM=ABtanC,CM=ACtanCBM = AB \tan C,\quad CM = AC \tan CBM=ABtanC,CM=ACtanCLại có:
CN=ACCN = ACCN=ACThay vào biểu thức:
CM⋅BMCN=(ACtanC)(ABtanC)AC=ABtan2CtanC=tan3C\frac{CM \cdot BM}{CN} = \frac{(AC\tan C)(AB\tan C)}{AC} = AB \tan^2 C \tan C = \tan^3 CCNCM⋅BM=AC(ACtanC)(ABtanC)=ABtan2CtanC=tan3C
✅ Kết luận câu c
CM⋅BMCN=tan3C\boxed{\frac{CM \cdot BM}{CN} = \tan^3 C}CNCM⋅BM=tan3C
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
12205
Đã trả lời bởi chuyên gia
12205 -
 Đã trả lời bởi chuyên gia
4995
Đã trả lời bởi chuyên gia
4995 -
 Đã trả lời bởi chuyên gia
3349
Đã trả lời bởi chuyên gia
3349 -
 Đã trả lời bởi chuyên gia
2059
Đã trả lời bởi chuyên gia
2059