Cho tg ABC vuông tại A. Đường phân giác của góc ABC cắt AC tại H. Kẻ HE vuông góc với BC (E thuộc BC). Đường thẳng EH và BA cắt nhau tại I.
a) CM: tg ABH = tg EBH.
b) CM: BH là trung trực của AE.
c) CM: tg HIC cân.
d) Gọi M là giao điểm của AE và BH. Gọi F và K lần lượt là trung điểm của của IA và IE. CM I, G, M thẳng hàng, với G là giao điểm của AK và EF.
Quảng cáo
1 câu trả lời 531
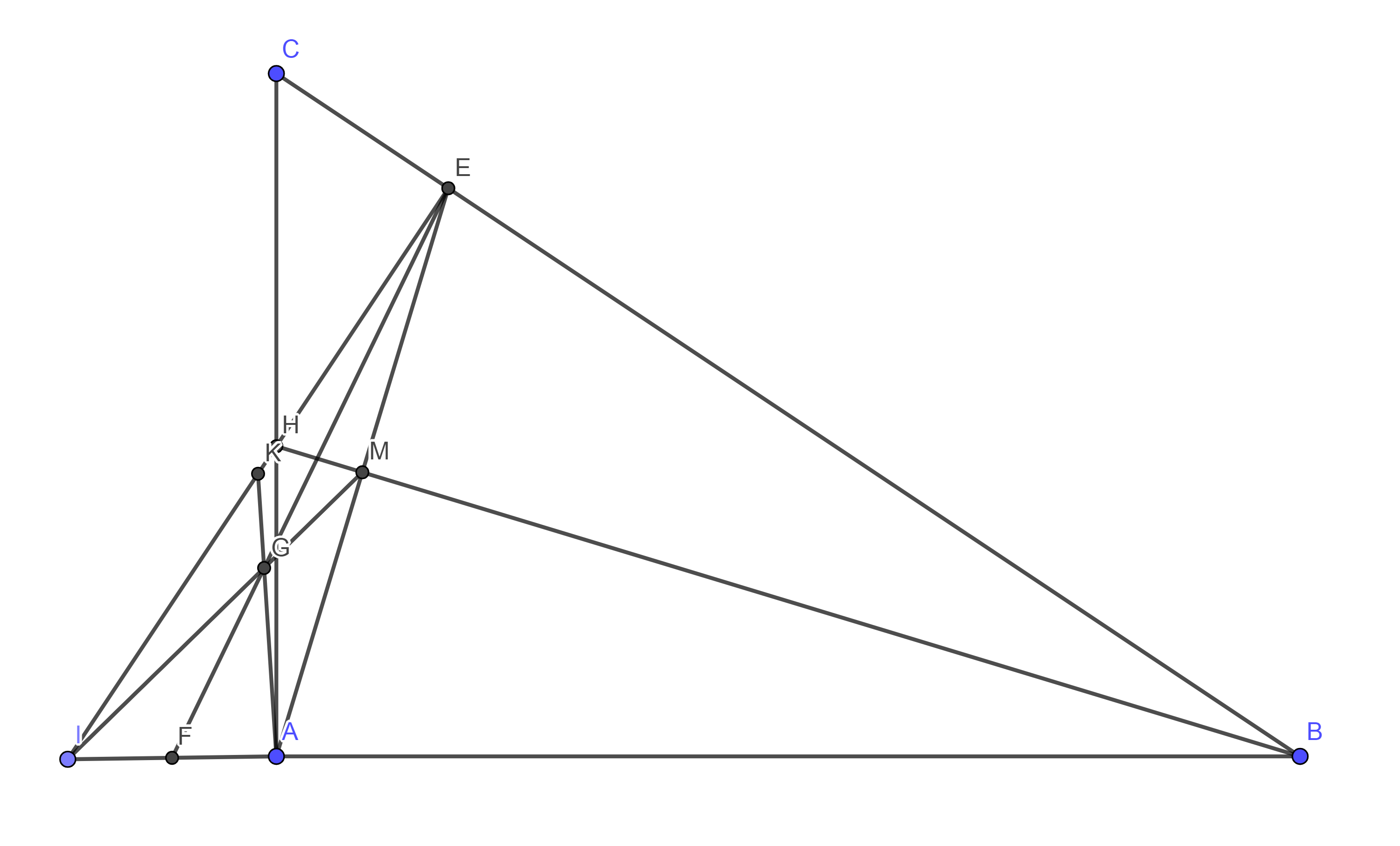
a.Xét ΔAHB và ΔEHB có
BH chung
∠ABH=∠EBH (gt)
⇒ ΔAHB = ΔEHB (ch-gn)
b. Do ΔAHB = ΔEHB
⇒AB=EB
⇒ΔEAB cân B
Mà BH là phân giác góc B
⇒BH đồng thời là đường trung trực AE
c) Xét tam giác ABC cs đường phân giác BH
=> CH/AH=BC/AB
ta có: Góc HCE+góc CHE=90
Mà góc HCE+góc ABC=90
Góc CHE=góc AHI(đối đỉnh)
=>Góc AHI=góc ABC
Xét tam giác AHI và tam giác ABC có:
Góc HAI=góc BAC=90
Góc AHI=góc ABC
=>Tam giác AHItam giác ABC
=> AH/HI=AB/BC
Hay HI/AH=BC/AB
Mà CH/AH=BC/AB
=>CH=HI
=>Tam giác CHI cân tại H
d) ta có ΔAHB = ΔEHB
=> BE=BA
=>Tam giác BAE cân tại B
Có BM là phân giác
=>BM đồng thời là trung tuyến
=> M là trung điểm của AE
Xét tam giác AEI có EF vfa AK là trung tuyến
EF cắt AK tại G
=>G là trọng tâm của tam giác AEI
Mà IM là trung tuyến (do M là trung điểm của AE)
=> G thuộc IM
Hay I;G;M thẳng hàng (đpcm)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
12381
-
 Đã trả lời bởi chuyên gia
5734
Đã trả lời bởi chuyên gia
5734 -
4829


