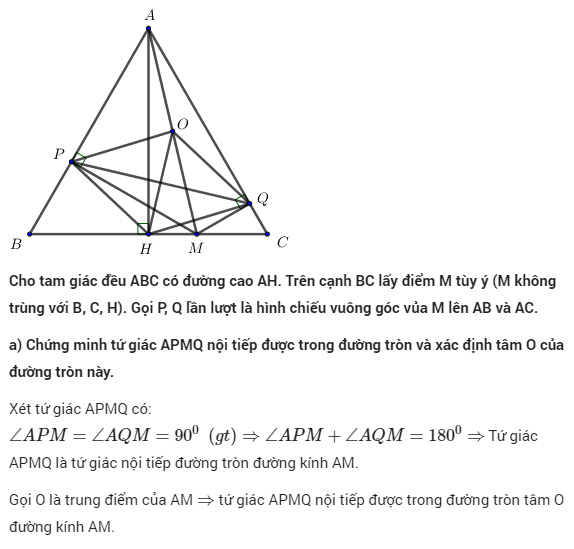
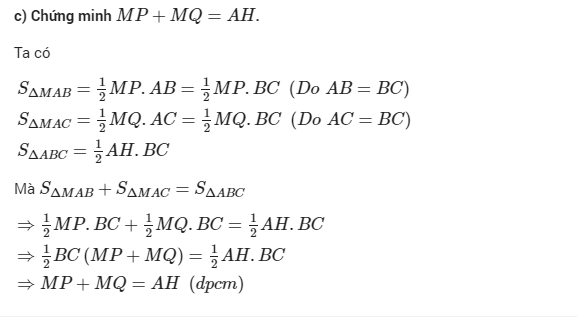Cho tam giác đều ABC có đường cao AH (H thuộc BC). Trên cạnh BC lấy điểm M (M không trùng với B, C, H). Gọi P và Q lần lượt là hình chiếu vuông góc của M trên hai cạnh AB và AC.
a) Chứng minh rằng 5 điểm A, P, H, M, Q cùng nằm trên một đường tròn tâm O.
b) Chứng minh rằng tam giác OHQ đều. Từ đó hãy suy ra OH vuông góc với PQ.
c) Chứng minh rằng MP + MQ = AH.
Quảng cáo
2 câu trả lời 6227
bạn có thể tham khảo link này
https://tuhoc365.vn/qa/cho-tam-giac-deu-abc-co-duong-cao-ah-tren-canh-bc-lay-diem-m-tuy-y-m/
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
8450
Đã trả lời bởi chuyên gia
8450 -
 Đã trả lời bởi chuyên gia
7975
Đã trả lời bởi chuyên gia
7975 -
 Đã trả lời bởi chuyên gia
5915
Đã trả lời bởi chuyên gia
5915
Gửi báo cáo thành công!