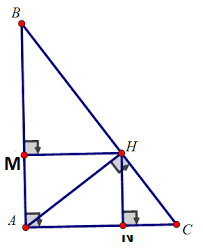
Cho tam giác ABC vuông tại A. Biết AB = 9cm, BC = 15cm. a/ Giải tam giác vuông ABC. ( cạnh làm tròn đến chữ số thập phân thứ nhất, góc làm tròn đến độ) b/Kẻ đường cao AH, điểm M và N lần lượt là hình chiếu của H lên AB và AC. Chứng minh: HN.AB = HM.AC(không dùng độ dài để chứng minh)
Quảng cáo
2 câu trả lời 7986
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
8450
Đã trả lời bởi chuyên gia
8450 -
 Đã trả lời bởi chuyên gia
6212
Đã trả lời bởi chuyên gia
6212 -
 Đã trả lời bởi chuyên gia
5915
Đã trả lời bởi chuyên gia
5915
Gửi báo cáo thành công!