Tìm số nguyên x, y biết:
Quảng cáo
2 câu trả lời 9962
Giải chi tiết:
Bước 1: Quy đồng mẫu phương trình
Ta quy đồng mẫu:
Mẫu chung là 6, nên:
Gộp phân số ở vế phải:
Bước 2: Đảo phân số
Lấy nghịch đảo hai vế:
Bước 3: Điều kiện để x là số nguyên
Để x là số nguyên, 1 + 2y phải là ước của 6. Các ước của là:
Bước 4: Xét từng trường hợp
- 1 + 2y = 1:
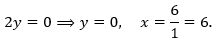
- 1 + 2y = -1:
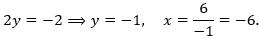
- 1 = 2y = 2:
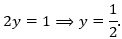
(Loại vì y không nguyên).
- 1 + 2y = -2:
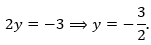
(Loại vì y không nguyên).
- 1 + 2y = 3:
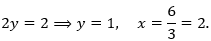
- 1 + 2y = -3:
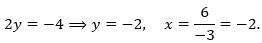
- 1 + 2y = 6
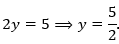
(Loại vì y không nguyên).
- 1 + 2y = -6
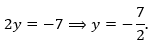
(Loại vì y không nguyên).
Bước 5: Kết luận
Các nghiệm nguyên x, y là:
$\dfrac{1}{x} = \dfrac{1}{6} + \dfrac{y}{3}$
$\dfrac{1}{x} = \dfrac{1}{6} + \dfrac{2y}{6}$
$\dfrac{1}{x} = \dfrac{2y + 1}{6}$
$x(2y + 1) = 6$
Vì $y$ nguyên nên $2y + 1$ là số lẻ
Vì $x, y$ nguyên nên $x, 2y + 1$ nguyên
Suy ra $x, 2y + 1$ là ước của $6$
Mà $2y + 1$ là số lẻ nên ta lập được bảng sau:
$\begin{array}{|c|c|c|} \hline \text{$x$}&\text{$-2$}&\text{$-6$}&\text{$6$}&\text{$2$}
\\\hline \text{$2y + 1$}&\text{$-3$}&\text{$-1$}&\text{$1$}&\text{$3$}
\\\hline \text{$y$}&\text{$-2$}&\text{$-1$}&\text{$0$}&\text{$1$} \\\hline \end{array}$
Vậy các cặp $(x; y)$ nguyên thoả mãn là $(-2; -2), (-6; -1), (6; 0), (2; 1)$
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
2235 điểm
-
I miss you
2045 điểm
-
𓇼 ⋆.˚annabelle⋆.˚ 𓇼 1260 điểm
-
Judy Hopps
1100 điểm
-
bích hồng nguyễn 760 điểm
-
`color{red}text{HuyTùng`
530 điểm
-
zai đẹp siu
490 điểm
-
lọ hà nội
440 điểm
-
dũng ngon hơn ok
405 điểm
-
Haruto[pad] 395 điểm
-
chê ng tốt chốt ng tồi.
365 điểm
-
n.t.an
300 điểm
-
⋅˚₊‧ ଳ⋆.࿔*:･𝙇ệ_ဗီူ_𝙥𝙝𝙪_ဗီူ_𝙣𝙝â𝙣⋅˚₊‧ ଳ⋆.࿔*:･
245 điểm
-
minhxinhquama
190 điểm
-
✿ 𝓝𝓪̂́𝓶 🍄
180 điểm
Rút gọn
Bài viết mới nhất Lớp 7
-
2 năm trước4926
