Cho tam giác nhọn ABC (AB < AC) có góc A bằng 600. D là trung điểm của cạnh AC. Trên tia AB lấy điểm E sao cho AE = AD. Chứng minh rằng:
a) tam giác ADE là tam giác đều.
b) tam giác DEC là tam giác cân.
c) CE vuông góc AB.
Quảng cáo
3 câu trả lời 2971
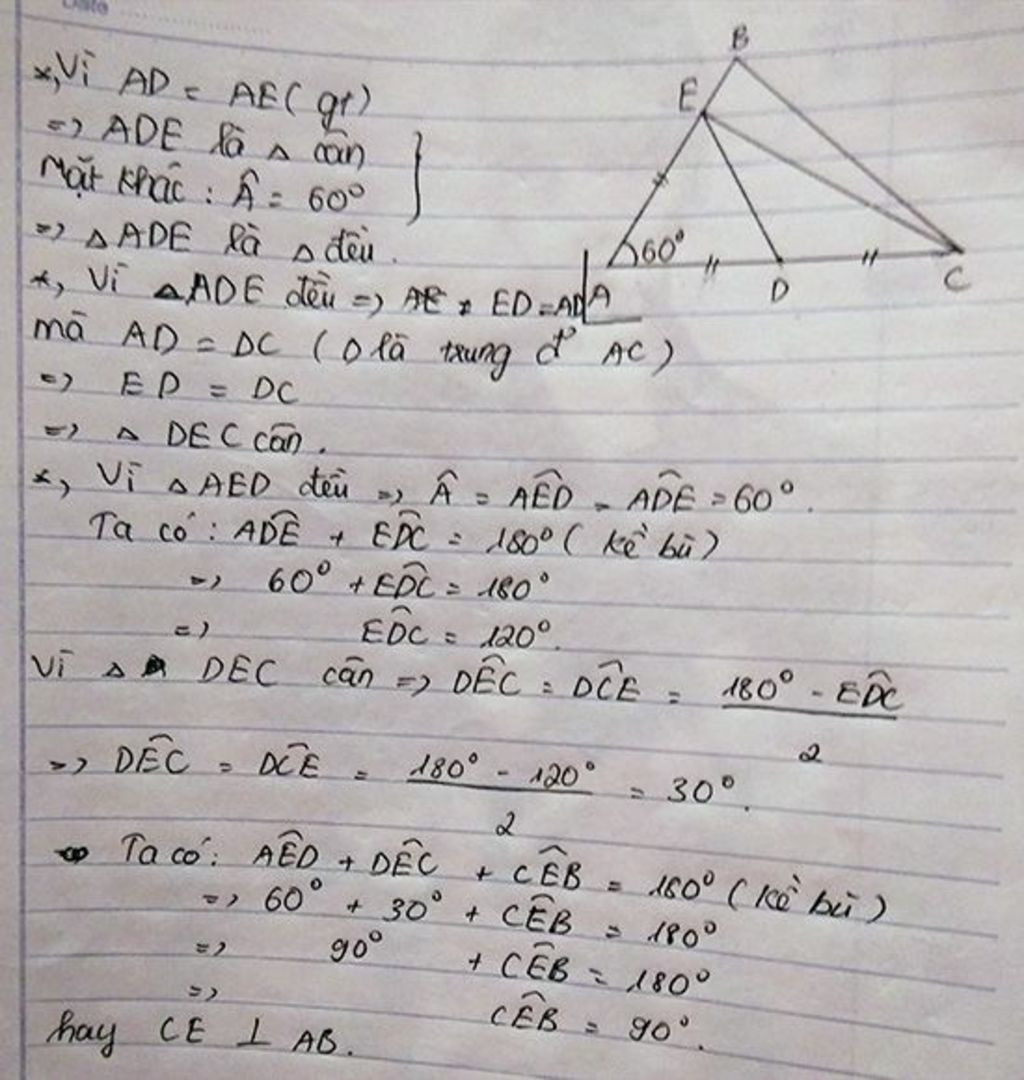
ĐÂY NHÉ
Lâm Mộc
· 4 năm trước
a) Vì AE=AD nên tam giác ADE cân tại A ; mà A=60 độ . Vậy tam giác ADE là tam giác đều b) Tam giác ADE là tam giác đều => AD=DE ; mà AD=DC ( D là trung điểm AC)=> DE=DC=> tam giác DEC cân tại D c) ADB+BDC=180 độ (kề bù)=>BDC=180-ADB=180-60=120 = DBC=DCB= 180 − 120 2 =30 AEC=ABD+DBC=60+30=90 .Vậy CE vuông góc AB . hình bạn tự vẽ nha
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757
Gửi báo cáo thành công!


