Quảng cáo
4 câu trả lời 810
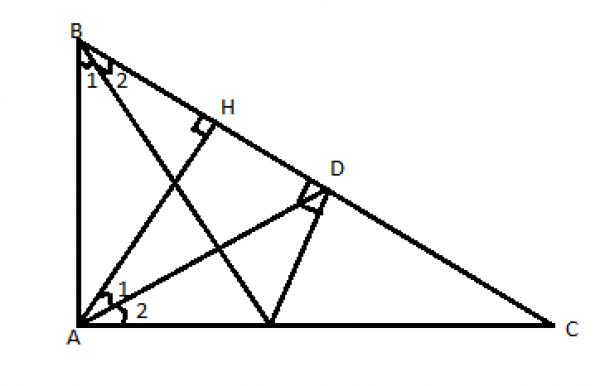
xét ABE và ∆ DBF có:
BE là cạnh chung
(BE là tia phân giác)
=> ∆ABE = ∆ DBE (cạn huyền - góc nhọn)
=> AE=DE (2 cạnh tương ứng)
=> ∆ AED là ∆ cân
có (Quan hệ song song)
(Cặp góc so le trong)
mà (cmt)
=> AD là tia phân giác của
tam giác ABE = tam giác DBE ( C. huyền- g. nhọn) ( tự chứng minh)
=> AE=ED
=> tam giác AED cân tại E => góc EAD= góc EDA (1)
lại có : AH và ED vuông với BC => AH // ED
=> góc HAD = góc ADE (2)
từ (1) và (2) => góc HAD = góc DAE ( cừng bằng góc ADE)
hay AD là tia phân giác của góc HAC (dpcm)
xét Δ∆ABE và ∆ DBF có:
ˆBAE=ˆBDE(90o)
BE là cạnh chung
ˆB1=ˆB2(BE là tia phân giác)
=> ∆ABE = ∆ DBE (cạn huyền - góc nhọn)
=> AE=DE (2 cạnh tương ứng)
=> ∆ AED là ∆ cân
có AH⊥BCED⊥BC}⇒AH//EDAH⊥BCED⊥BC⇒AH//ED(Quan hệ song song)
⇒ˆA1 = ˆADE(Cặp góc so le trong)
mà ˆA2=ˆADE(cmt)
⇒ˆA1=ˆA2
=> AD là tia phân giác của ˆHAC
xét Δ∆ABE và ∆ DBF có:
ˆBAE=ˆBDE(90o)
BE là cạnh chung
ˆB1=ˆB2(BE là tia phân giác)
=> ∆ABE = ∆ DBE (cạn huyền - góc nhọn)
=> AE=DE (2 cạnh tương ứng)
=> ∆ AED là ∆ cân
có AH⊥BCED⊥BC}⇒AH//EDAH⊥BCED⊥BC⇒AH//ED(Quan hệ song song)
⇒ˆA1 = ˆADE(Cặp góc so le trong)
mà ˆA2=ˆADE(cmt)
⇒ˆA1=ˆA2
=> AD là tia phân giác của ˆHAC
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757


