Cho tam giác ABC ( AB > AC ) nhọn, kẻ AH vuông góc với BC, (H thuộc BC) gọi M là một điểm nằm giữa A và H tia BM cắt AC ở D. Chứng minh rằng:
a) BM > CM và
b) DM < DH
Quảng cáo
1 câu trả lời 124
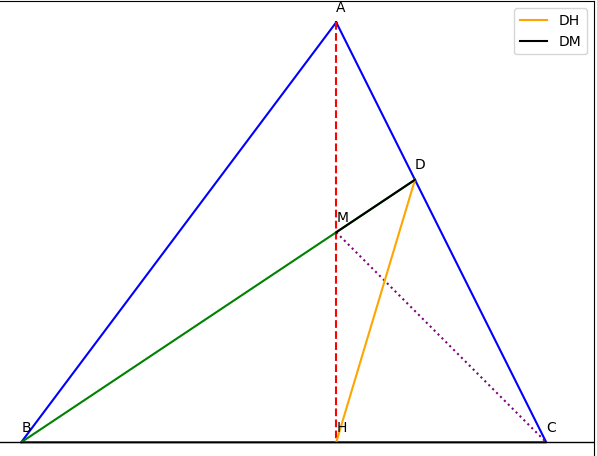
a) Chứng minh BM > CM và
- Xét ABC nhọn có AH BC.
Vì AB > AC (đường xiên lớn hơn) => HB > HC (hình chiếu lớn hơn).
- Xét MBC có MH BC. Vì HB > HC (hình chiếu lớn hơn)
=> MB > MC (đường xiên lớn hơn).
- Trong MHB và MHC vuông tại H, có chung cạnh MH.
Vì HB > HC => góc đối diện .
b) Chứng minh DM < DH
- Xét MHD vuông tại H (với D là điểm trên AC sao cho hình chiếu của D lên AH nằm giữa M và A):
- Trong tam giác vuông, cạnh huyền luôn là cạnh lớn nhất.
- Tuy nhiên, xét vị trí hình học: M nằm giữa A và H, D thuộc AC. Khi đó MH là đường vuông góc, MD là đường xiên.
- Vì M gần H hơn so với hình chiếu của D trên đường thẳng AH, theo quan hệ đường vuông góc - đường xiên: DM < DH.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK122604
-
 Đã trả lời bởi chuyên gia
83098
Đã trả lời bởi chuyên gia
83098 -
 Đã trả lời bởi chuyên gia
62086
Đã trả lời bởi chuyên gia
62086 -
 Đã trả lời bởi chuyên gia
40251
Đã trả lời bởi chuyên gia
40251


