Cho tam giác ABC cho góc A = 90° và BC = 2.AB, E là trung điểm của BC. Tia phân giác của góc B cắt cạnh AC ở D
a) Chứng minh DB là phân giác của góc ADE
b) Chứng minh BD = DC
c) Tính góc B và góc C trong tam giác ABC
Quảng cáo
1 câu trả lời 173
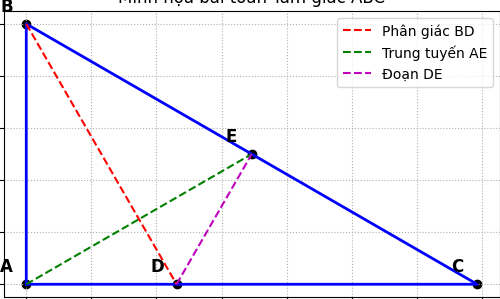
a) Chứng minh DB là phân giác của góc ADE)
- Xét ABE: Ta có AB = BE (theo giả thiết và cách lấy điểm $E$).
Do đó, ABE cân tại B.
- Xét ABD và EBD, ta có:
AB = EB (chứng minh trên).
(vì BD là tia phân giác của ).
Cạnh BD chung.
=> ABD = EBD (cạnh - góc - cạnh).
- Từ hai tam giác bằng nhau, ta suy ra các cặp cạnh và góc tương ứng:
AD = ED => ADE cân tại D.
.
- Vì ADE cân tại D, nên đường cao xuất phát từ đỉnh D đồng thời là đường phân giác. Tuy nhiên, cách nhanh nhất là xét ta có
Vậy: DB là tia phân giác của .
b) Chứng minh BD = DC
- Xét ABC vuông tại A có BC = 2AB:
- Đây là tính chất đặc biệt. Trong tam giác vuông, nếu cạnh huyền gấp đôi một cạnh góc vuông thì góc đối diện với cạnh góc vuông đó bằng 30.
- Xét tổng các góc trong ABC:
.
- Vì BD là phân giác của nên:
.
- Xét BDC có:
=> cân tại D.
Vậy: BD = DC.
c) Tính góc B và góc C trong tam giác ABC
Như đã chứng minh ở câu (b) dựa trên tỉ lệ cạnh:
.
=> .
=> .
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK123713
-
 Đã trả lời bởi chuyên gia
83420
Đã trả lời bởi chuyên gia
83420 -
 Đã trả lời bởi chuyên gia
62842
Đã trả lời bởi chuyên gia
62842 -
 Đã trả lời bởi chuyên gia
40435
Đã trả lời bởi chuyên gia
40435 -
 Đã trả lời bởi chuyên gia
36962
Đã trả lời bởi chuyên gia
36962


