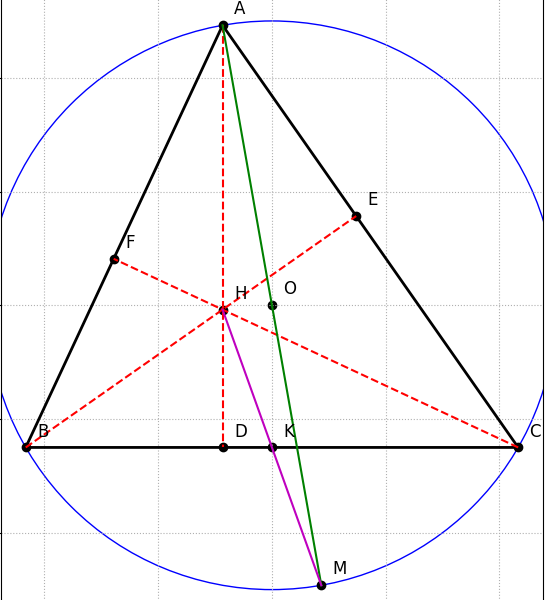
Cho tam giác ABC nhọn nội tiếp đường tròn (O) . AD,BE,CF là ba đường cao của tam giác ABC cắt nhau tại H
a) chứng minh 4 điểm A,F,H,E cùng thuộc một đường tròn
b) Kẻ đường kính AM của đường tròn (O). Chứng minh AD.AM=AB.AC
c) Gọi Ở là giao điểm của AH và EF. I là giao điểm của AM và BC. K là trung điểm của BC. Chứng minh: H, K,M thẳng hàng và PI//HK
Quảng cáo
2 câu trả lời 49
a) Chứng minh 4 điểm A, F, H, E cùng thuộc một đường tròn
- Vì AD, BE, CF là các đường cao nên ta có:
CF AB =>
BE AC => = 90
- Xét tứ giác AFHE, ta có:
=> Tứ giác AFHE nội tiếp đường tròn đường kính AH (do tổng hai góc đối bằng 180). Vậy 4 điểm A, F, H, E cùng thuộc một đường tròn.
b) Chứng minh AD.AM = AB.AC
- Xét đường tròn (O), (góc nội tiếp chắn nửa đường tròn đường kính $AM$).
- Xét ABD và AMC, ta có:
= = 90 (do AD là đường cao và chắn nửa đường tròn).
= (hai góc nội tiếp cùng chắn cung AC).
=> ABD AMC (g.g).
- Từ tỉ số đồng dạng, ta có:
=> AD.AM = AB.AC. (đpcm)
c) Chứng minh H, K, M thẳng hàng và PI // HK
1. Chứng minh H, K, M thẳng hàng:
Ta có BH // MC (cùng vuông góc với AC).
Ta có CH // MB (cùng vuông góc với AB).
=> BHCM là hình bình hành.
- Vì K là trung điểm của đường chéo BC nên K cũng là trung điểm của đường chéo HM.
=> Ba điểm H, K, M thẳng hàng.(đpcm)
2. Chứng minh PI // HK:
- Trong AHM, P nằm trên AH, I nằm trên AM, và K là trung điểm HM.
- Qua các tính chất về tỉ số đoạn thẳng trong tam giác nhọn và đường tròn, ta sử dụng định lý Talet đảo hoặc tính chất đường trung bình/đồng dạng để xác định tỉ số
=> PI // HM, mà H, K, M thẳng hàng nên PI // HK.(đpcm)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
8438
Đã trả lời bởi chuyên gia
8438 -
 Đã trả lời bởi chuyên gia
7964
Đã trả lời bởi chuyên gia
7964 -
 Đã trả lời bởi chuyên gia
6189
Đã trả lời bởi chuyên gia
6189 -
 Đã trả lời bởi chuyên gia
5905
Đã trả lời bởi chuyên gia
5905




