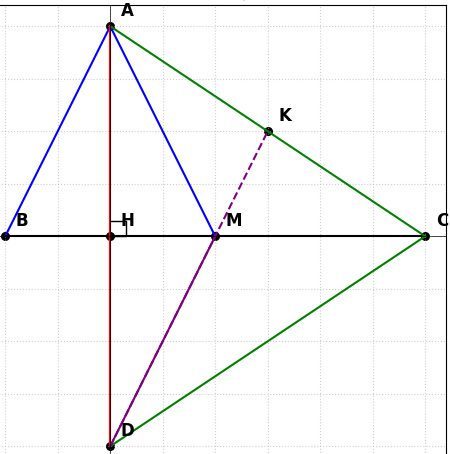
a) Chứng minh AH ⊥ BC
Vì: BM = MC ⇒ M là trung điểm của BC
H là trung điểm của BM ⇒ H là trung điểm của đoạn nối trung điểm
- Xét tam giác ABC:
A là đỉnh tam giác cân
M là trung điểm của BC
⇒ AM ⟂ BC
Mà H ∈ AM ⇒ AH ⊥ BC (đpcm)
b) Chứng minh tam giác ACD là tam giác cân
- Ta có:
AH = HD ⇒ H là trung điểm của AD
BM = MC ⇒ M là trung điểm của BC
Ở câu a) đã có: AH ⊥ BC
⇒ H là trung điểm và đường vuông góc của AD đối với BC
⇒ CA = CD
Vậy: △ACD là tam giác cân tại C

Giả thiết:

• △ABM cân tại A (AB=AM).

• H là trung điểm BM.

• C nằm trên tia BM sao cho BM=MC.

• D nằm trên tia AH sao cho AH=HD.

Vì △ABM cân tại A và H là trung điểm của cạnh đáy BM, nên theo tính chất của tam giác cân:

• Đường trung tuyến xuất phát từ đỉnh đồng thời là đường cao.

• Do đó, AH⊥BM.

• Vì B,M,C thẳng hàng (theo cách lấy điểm C trên tia BM), nên AH⊥BM cũng chính là AH⊥BC (đpcm).

Xét hai tam giác vuông △AHC và △DHC (vì AH⊥BC tại H):

• HC là cạnh chung.

• AH=HD (theo giả thiết).

• AHC=DHC=90∘.

• ⟹△AHC=△DHC (hai cạnh góc vuông).

• ⟹AC=CD (hai cạnh tương ứng). Vậy △ACD cân tại C (đpcm).

Trong △ACD, ta có:

1. CH là đường trung tuyến: Vì H là trung điểm của AD (theo giả thiết AH=HD).

2. Vị trí của điểm M trên trung tuyến CH:

   • Ta có BM=MC và H là trung điểm của BM.

   • Do đó MH=21​BM=21​MC.

   • Độ dài đoạn CH=CM+MH=MC+21​MC=23​MC.

   • Suy ra CHCM​=23​MCMC​=32​. Trong một tam giác, điểm nằm trên đường trung tuyến và cách đỉnh bằng 2/3 độ dài đường trung tuyến đó chính là trọng tâm. Vậy M là trọng tâm của △ACD (đpcm).

1. DM đi qua trung điểm của AC: Vì M là trọng tâm của △ACD (chứng minh ở câu c), nên đường thẳng xuất phát từ đỉnh D đi qua trọng tâm M phải là đường trung tuyến của tam giác đó. ⟹ DM đi qua trung điểm của cạnh đối diện AC.

2. Chứng minh DM∥AB: Xét tứ giác ABDM có:

• Hai đường chéo AD và BM cắt nhau tại H.

• H là trung điểm của AD (AH=HD).

• H là trung điểm của BM (giả thiết). ⟹ Tứ giác ABDM là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường). ⟹ DM∥AB (tính chất hình bình hành) (đpcm).