Câu 5 : Cho △ABC vuông tại A. Trên tia đối tia AB lấy điểm D sao cho AD = AB.
a) (TH) Chứng minh: △ABC = △ADC.
b) (TH) Từ A kẻ đường thẳng song song với BC cắt CD tại M. Chứng minh: MA = MC.
c) (VDC) Chứng minh: MA = CD
Quảng cáo
1 câu trả lời 64
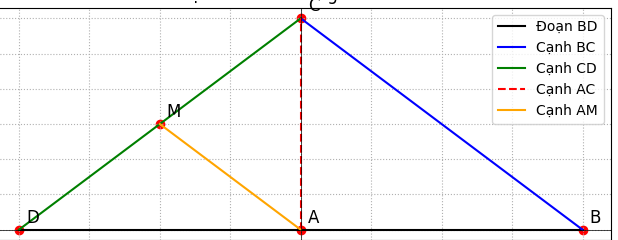
a. Chứng minh ABC = ADC
- Xét hai tam giác vuông ABC và ADC có:
AB = AD (theo giả thiết).
(do AC AB và D thuộc tia đối của AB).
AC là cạnh chung.
=> ABC = ADC (cạnh - góc - cạnh).
b. Chứng minh MA = MC
- Từ kết quả câu (a), ta có CB = CD (hai cạnh tương ứng)
=> BCD cân tại C.
- Vì AM // BC, nên theo tính chất góc so le trong và đồng vị:
(so le trong).
(đồng vị).
- Vì ABC = ADC nên .
=> (vì cùng bằng ).
=> Tam giác MAC cân tại M, do đó MA = MC.(đpcm)
c. Chứng minh MA =CD
Ta đã có MA = MC (1).
Lại có (đồng vị do AM // BC).
Mà (do ABC = ADC).
=> hay (điều này hiển nhiên). Tuy nhiên, xét tam giác MAD, ta có: (so le trong với góc B nếu xét kỹ hơn hoặc dùng tính chất phụ nhau).
- Thực tế, trong tam giác vuông ADC, M là trung điểm của CD.
- Vì MA = MC và qua tính chất góc, ta cũng chứng minh được MA = MD.
Vậy MA = MC = MD = CD. (đpcm)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK122114
-
 Đã trả lời bởi chuyên gia
82864
Đã trả lời bởi chuyên gia
82864 -
 Đã trả lời bởi chuyên gia
61136
Đã trả lời bởi chuyên gia
61136 -
 Đã trả lời bởi chuyên gia
40104
Đã trả lời bởi chuyên gia
40104


