Thị Hảo Nguyễn
Hỏi từ APP VIETJACK
Cho xAy =60°,AZ là tia phân giác ,lấy B€ tia AZ.Qua B vẽ đường thẳng // Ay cắt Ax tại C,đường thẳng // Ax cắt Ay tại D
a) chứng minh AC=AD;BC=BD
Vẽ hình luôn
a) chứng minh AC=AD;BC=BD
Vẽ hình luôn
`d.`
· 2 tuần trước
kia là bc hay be v?
Quảng cáo
2 câu trả lời 75
2 tuần trước
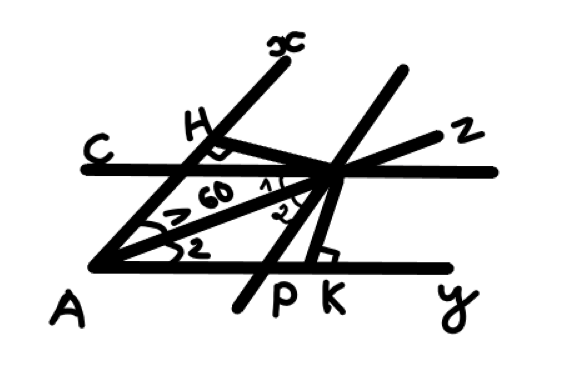
`a)`
BD//AC
=>DBA^=BAC^DBA=BAC(hai góc so le trong)(1)
CB//AD
=>CBA^=DAB^CBA=DAB(hai góc so le trong)(2)
AB là phân giác của góc CAD
=>CAB^=DAB^(3)CAB=DAB(3)
Từ (1),(2),(3) suy ra DBA^=CBA^DBA=CBA
Xét ΔACB và ΔADB có
DBA^=CBA^DBA=CBA
BA chung
CAB^=DAB^CAB=DAB
Do đó: ΔACB=ΔADB
=>AC=AD và BC=BD
2 tuần trước
Chứng minh AC=ADcap A cap C equals cap A cap D
𝐴𝐶=𝐴𝐷
và BC=BDcap B cap C equals cap B cap D
𝐵𝐶=𝐵𝐷
Các bước giải
Xác định các góc được tạo bởi tia phân giác và các đường thẳng song song.
Sử dụng tính chất của tia phân giác để suy ra các góc bằng nhau.
Sử dụng tính chất của các đường thẳng song song để suy ra các góc so le trong bằng nhau.
Chứng minh tam giác ABCcap A cap B cap C
𝐴𝐵𝐶
và tam giác ABDcap A cap B cap D
𝐴𝐵𝐷
là các tam giác cân.
Từ đó suy ra các cạnh bằng nhau.
Lời giải chi tiết
Vì AZcap A cap Z
𝐴𝑍
là tia phân giác của góc xAŷmodifying-above x cap A y with hat
𝑥𝐴𝑦
nên xAẐ=yAẐ=xAŷ2=60∘2=30∘modifying-above x cap A cap Z with hat equals modifying-above y cap A cap Z with hat equals the fraction with numerator modifying-above x cap A y with hat and denominator 2 end-fraction equals the fraction with numerator 60 raised to the exponent composed with end-exponent and denominator 2 end-fraction equals 30 raised to the exponent composed with end-exponent
𝑥𝐴𝑍=𝑦𝐴𝑍=𝑥𝐴𝑦2=60∘2=30∘
.
Vì BC∥Aycap B cap C is parallel to cap A y
𝐵𝐶∥𝐴𝑦
nên ACB̂=yAẐ=30∘modifying-above cap A cap C cap B with hat equals modifying-above y cap A cap Z with hat equals 30 raised to the exponent composed with end-exponent
𝐴𝐶𝐵=𝑦𝐴𝑍=30∘
(hai góc so le trong).
Xét tam giác ABCcap A cap B cap C
𝐴𝐵𝐶
, có BAĈ=xAŷ=60∘modifying-above cap B cap A cap C with hat equals modifying-above x cap A y with hat equals 60 raised to the exponent composed with end-exponent
𝐵𝐴𝐶=𝑥𝐴𝑦=60∘
và ACB̂=30∘modifying-above cap A cap C cap B with hat equals 30 raised to the exponent composed with end-exponent
𝐴𝐶𝐵=30∘
.
Tính góc ABĈ=180∘−BAĈ−ACB̂=180∘−60∘−30∘=90∘modifying-above cap A cap B cap C with hat equals 180 raised to the exponent composed with end-exponent minus modifying-above cap B cap A cap C with hat minus modifying-above cap A cap C cap B with hat equals 180 raised to the exponent composed with end-exponent minus 60 raised to the exponent composed with end-exponent minus 30 raised to the exponent composed with end-exponent equals 90 raised to the exponent composed with end-exponent
𝐴𝐵𝐶=180∘−𝐵𝐴𝐶−𝐴𝐶𝐵=180∘−60∘−30∘=90∘
.
Vì BD∥Axcap B cap D is parallel to cap A x
𝐵𝐷∥𝐴𝑥
nên ADB̂=xAẐ=30∘modifying-above cap A cap D cap B with hat equals modifying-above x cap A cap Z with hat equals 30 raised to the exponent composed with end-exponent
𝐴𝐷𝐵=𝑥𝐴𝑍=30∘
(hai góc so le trong).
Xét tam giác ABDcap A cap B cap D
𝐴𝐵𝐷
, có BAD̂=xAŷ=60∘modifying-above cap B cap A cap D with hat equals modifying-above x cap A y with hat equals 60 raised to the exponent composed with end-exponent
𝐵𝐴𝐷=𝑥𝐴𝑦=60∘
và ADB̂=30∘modifying-above cap A cap D cap B with hat equals 30 raised to the exponent composed with end-exponent
𝐴𝐷𝐵=30∘
.
Tính góc ABD̂=180∘−BAD̂−ADB̂=180∘−60∘−30∘=90∘modifying-above cap A cap B cap D with hat equals 180 raised to the exponent composed with end-exponent minus modifying-above cap B cap A cap D with hat minus modifying-above cap A cap D cap B with hat equals 180 raised to the exponent composed with end-exponent minus 60 raised to the exponent composed with end-exponent minus 30 raised to the exponent composed with end-exponent equals 90 raised to the exponent composed with end-exponent
𝐴𝐵𝐷=180∘−𝐵𝐴𝐷−𝐴𝐷𝐵=180∘−60∘−30∘=90∘
.
Xét tam giác ABCcap A cap B cap C
𝐴𝐵𝐶
và tam giác ABDcap A cap B cap D
𝐴𝐵𝐷
, có cạnh ABcap A cap B
𝐴𝐵
chung, BAĈ=BAD̂=60∘modifying-above cap B cap A cap C with hat equals modifying-above cap B cap A cap D with hat equals 60 raised to the exponent composed with end-exponent
𝐵𝐴𝐶=𝐵𝐴𝐷=60∘
và ACB̂=ADB̂=30∘modifying-above cap A cap C cap B with hat equals modifying-above cap A cap D cap B with hat equals 30 raised to the exponent composed with end-exponent
𝐴𝐶𝐵=𝐴𝐷𝐵=30∘
.
Do đó, △ABC=△ABDtriangle cap A cap B cap C equals triangle cap A cap B cap D
△𝐴𝐵𝐶=△𝐴𝐵𝐷
(g.c.g).
Từ đó suy ra AC=ADcap A cap C equals cap A cap D
𝐴𝐶=𝐴𝐷
và BC=BDcap B cap C equals cap B cap D
𝐵𝐶=𝐵𝐷
(các cạnh tương ứng).
Đáp án cuối cùng
AC=ADcap A cap C equals cap A cap D
𝐴𝐶=𝐴𝐷
và BC=BDcap B cap C equals cap B cap D
𝐵𝐶=𝐵𝐷
được chứng minh dựa trên sự bằng nhau của hai tam giác △ABCtriangle cap A cap B cap C
△𝐴𝐵𝐶
và △ABDtriangle cap A cap B cap D
△𝐴𝐵𝐷
.
𝐴𝐶=𝐴𝐷
và BC=BDcap B cap C equals cap B cap D
𝐵𝐶=𝐵𝐷
Các bước giải
Xác định các góc được tạo bởi tia phân giác và các đường thẳng song song.
Sử dụng tính chất của tia phân giác để suy ra các góc bằng nhau.
Sử dụng tính chất của các đường thẳng song song để suy ra các góc so le trong bằng nhau.
Chứng minh tam giác ABCcap A cap B cap C
𝐴𝐵𝐶
và tam giác ABDcap A cap B cap D
𝐴𝐵𝐷
là các tam giác cân.
Từ đó suy ra các cạnh bằng nhau.
Lời giải chi tiết
Vì AZcap A cap Z
𝐴𝑍
là tia phân giác của góc xAŷmodifying-above x cap A y with hat
𝑥𝐴𝑦
nên xAẐ=yAẐ=xAŷ2=60∘2=30∘modifying-above x cap A cap Z with hat equals modifying-above y cap A cap Z with hat equals the fraction with numerator modifying-above x cap A y with hat and denominator 2 end-fraction equals the fraction with numerator 60 raised to the exponent composed with end-exponent and denominator 2 end-fraction equals 30 raised to the exponent composed with end-exponent
𝑥𝐴𝑍=𝑦𝐴𝑍=𝑥𝐴𝑦2=60∘2=30∘
.
Vì BC∥Aycap B cap C is parallel to cap A y
𝐵𝐶∥𝐴𝑦
nên ACB̂=yAẐ=30∘modifying-above cap A cap C cap B with hat equals modifying-above y cap A cap Z with hat equals 30 raised to the exponent composed with end-exponent
𝐴𝐶𝐵=𝑦𝐴𝑍=30∘
(hai góc so le trong).
Xét tam giác ABCcap A cap B cap C
𝐴𝐵𝐶
, có BAĈ=xAŷ=60∘modifying-above cap B cap A cap C with hat equals modifying-above x cap A y with hat equals 60 raised to the exponent composed with end-exponent
𝐵𝐴𝐶=𝑥𝐴𝑦=60∘
và ACB̂=30∘modifying-above cap A cap C cap B with hat equals 30 raised to the exponent composed with end-exponent
𝐴𝐶𝐵=30∘
.
Tính góc ABĈ=180∘−BAĈ−ACB̂=180∘−60∘−30∘=90∘modifying-above cap A cap B cap C with hat equals 180 raised to the exponent composed with end-exponent minus modifying-above cap B cap A cap C with hat minus modifying-above cap A cap C cap B with hat equals 180 raised to the exponent composed with end-exponent minus 60 raised to the exponent composed with end-exponent minus 30 raised to the exponent composed with end-exponent equals 90 raised to the exponent composed with end-exponent
𝐴𝐵𝐶=180∘−𝐵𝐴𝐶−𝐴𝐶𝐵=180∘−60∘−30∘=90∘
.
Vì BD∥Axcap B cap D is parallel to cap A x
𝐵𝐷∥𝐴𝑥
nên ADB̂=xAẐ=30∘modifying-above cap A cap D cap B with hat equals modifying-above x cap A cap Z with hat equals 30 raised to the exponent composed with end-exponent
𝐴𝐷𝐵=𝑥𝐴𝑍=30∘
(hai góc so le trong).
Xét tam giác ABDcap A cap B cap D
𝐴𝐵𝐷
, có BAD̂=xAŷ=60∘modifying-above cap B cap A cap D with hat equals modifying-above x cap A y with hat equals 60 raised to the exponent composed with end-exponent
𝐵𝐴𝐷=𝑥𝐴𝑦=60∘
và ADB̂=30∘modifying-above cap A cap D cap B with hat equals 30 raised to the exponent composed with end-exponent
𝐴𝐷𝐵=30∘
.
Tính góc ABD̂=180∘−BAD̂−ADB̂=180∘−60∘−30∘=90∘modifying-above cap A cap B cap D with hat equals 180 raised to the exponent composed with end-exponent minus modifying-above cap B cap A cap D with hat minus modifying-above cap A cap D cap B with hat equals 180 raised to the exponent composed with end-exponent minus 60 raised to the exponent composed with end-exponent minus 30 raised to the exponent composed with end-exponent equals 90 raised to the exponent composed with end-exponent
𝐴𝐵𝐷=180∘−𝐵𝐴𝐷−𝐴𝐷𝐵=180∘−60∘−30∘=90∘
.
Xét tam giác ABCcap A cap B cap C
𝐴𝐵𝐶
và tam giác ABDcap A cap B cap D
𝐴𝐵𝐷
, có cạnh ABcap A cap B
𝐴𝐵
chung, BAĈ=BAD̂=60∘modifying-above cap B cap A cap C with hat equals modifying-above cap B cap A cap D with hat equals 60 raised to the exponent composed with end-exponent
𝐵𝐴𝐶=𝐵𝐴𝐷=60∘
và ACB̂=ADB̂=30∘modifying-above cap A cap C cap B with hat equals modifying-above cap A cap D cap B with hat equals 30 raised to the exponent composed with end-exponent
𝐴𝐶𝐵=𝐴𝐷𝐵=30∘
.
Do đó, △ABC=△ABDtriangle cap A cap B cap C equals triangle cap A cap B cap D
△𝐴𝐵𝐶=△𝐴𝐵𝐷
(g.c.g).
Từ đó suy ra AC=ADcap A cap C equals cap A cap D
𝐴𝐶=𝐴𝐷
và BC=BDcap B cap C equals cap B cap D
𝐵𝐶=𝐵𝐷
(các cạnh tương ứng).
Đáp án cuối cùng
AC=ADcap A cap C equals cap A cap D
𝐴𝐶=𝐴𝐷
và BC=BDcap B cap C equals cap B cap D
𝐵𝐶=𝐵𝐷
được chứng minh dựa trên sự bằng nhau của hai tam giác △ABCtriangle cap A cap B cap C
△𝐴𝐵𝐶
và △ABDtriangle cap A cap B cap D
△𝐴𝐵𝐷
.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669
Gửi báo cáo thành công!


