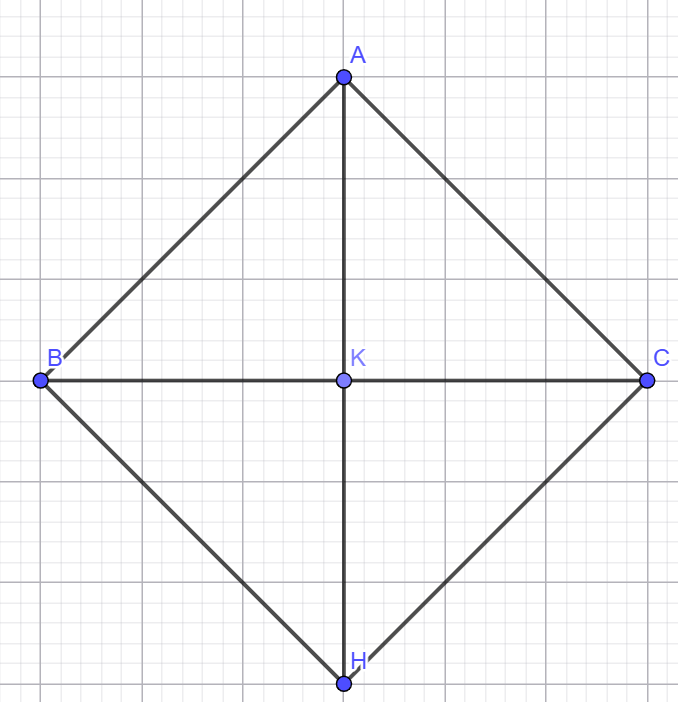
a) Ta có tam giác ABC có AB=AC nên Tam giác ABC cân tại A
$\widehat{ABC}=\widehat{ACB}$
Xét tam giác 
ABK và ACK có 
AB=AC ( gt)
$\widehat{ABC}=\widehat{ACB}$ ( cm trên)
BK=KC ( K là trung điểm BC)
$∆ABK=∆ACK ( c-g-c)$
b) Tam giác ABC cân tại A
Có AK là đường trung tuyến ứng với cạnh BC 
=> AK đồng thời là đường cao tam giác ABC
Xét tứ giác ABHC có
AK=KH
BK=KC
AH$\perp$BCtại K
nên ABHC là hình thoi ( 2 đường chéo vuông góc với nhau tại trung điểm mỗi đường ) 
=>AC//BH
c)

Chào bạn, đây là lời giải chi tiết cho bài hình học của bạn.

## 📐 Chứng minh Tam giác $\text{ABC}$ có $\text{AB} = \text{AC}$

### a) Chứng minh $\triangle ABK = \triangle ACK$

Xét $\triangle ABK$ và $\triangle ACK$ có:
* $\text{AB} = \text{AC}$ (giả thiết, $\triangle ABC$ cân tại $A$).
* $\text{AK}$ là cạnh chung.
* $\text{BK} = \text{CK}$ (vì $K$ là trung điểm của $BC$).

Vậy $\triangle ABK = \triangle ACK$ theo trường hợp **c.c.c** (cạnh - cạnh - cạnh).

---

### b) Chứng minh $\text{AC // HB}$

#### Cách 1: Dùng hai tam giác bằng nhau

* Vì $\triangle ABK = \triangle ACK$ (chứng minh ở câu a), suy ra $\text{góc } AKB = \text{góc } AKC$.
* Mà $\text{góc } AKB + \text{góc } AKC = 180^\circ$ (hai góc kề bù).
* Do đó, $\text{góc } AKB = \text{góc } AKC = 90^\circ$. Hay $\text{AK} \perp \text{BC}$.

Xét $\triangle ACK$ và $\triangle HBK$ có:
* $\text{AK} = \text{HK}$ (giả thiết).
* $\text{góc } AKC = \text{góc } HKB$ (hai góc đối đỉnh).
* $\text{CK} = \text{BK}$ (vì $K$ là trung điểm của $BC$).

Vậy $\triangle ACK = \triangle HBK$ theo trường hợp **c.g.c** (cạnh - góc - cạnh).

Suy ra $\text{góc } ACK = \text{góc } HBK$ (hai góc tương ứng).
Mà $\text{góc } ACK$ và $\text{góc } HBK$ ở vị trí **so le trong** đối với hai đường thẳng $\text{AC}$ và $\text{HB}$ bị đường thẳng $\text{BC}$ cắt.

Do đó, **$\text{AC // HB}$** (hai đường thẳng có cặp góc so le trong bằng nhau thì song song).

#### Cách 2: Dùng tứ giác $\text{ABHC}$

* Xét tứ giác $\text{ABHC}$ có hai đường chéo $\text{AH}$ và $\text{BC}$ cắt nhau tại trung điểm $K$ của mỗi đường ($\text{BK}=\text{CK}$, $\text{AK}=\text{HK}$).
* $\Rightarrow \text{ABHC}$ là **hình bình hành**.
* Trong hình bình hành, các cặp cạnh đối song song.
* Do đó, $\text{AC // HB}$ và $\text{AB // HC}$.

---

### c) Chứng minh ba điểm $\text{M}, \text{K}, \text{N}$ thẳng hàng

Chúng ta sẽ chứng minh $KM$ và $KN$ cùng vuông góc với đường thẳng $AH$ tại $K$.

#### Bước 1: Chứng minh $\text{KM} \perp \text{AH}$

* Vì $\triangle ABK = \triangle ACK$ (chứng minh ở câu a) và $\triangle ABC$ cân tại $A$, suy ra $AK$ là đường phân giác của $\text{góc } BAC$.
$\text{Góc } KAC = \text{Góc } KAB$
* Mặt khác, $K$ là trung điểm của $BC$ và $\triangle ABC$ cân tại $A$, nên $AK$ cũng là đường cao, hay $\text{AK} \perp \text{BC}$.
* $K$ nằm trên đường phân giác $AK$ của $\text{góc } BAC$.
* $KM \perp AC$ (giả thiết, $M \in AC$).
* Kẻ $KP \perp AB$ ($P \in AB$).
* Theo tính chất điểm thuộc đường phân giác, ta có **$KM = KP$**.

#### Bước 2: Chứng minh $\text{KN} \perp \text{AH}$

* Ta đã chứng minh **$\text{AC // HB}$** (ở câu b).
* Mà $\text{KM} \perp \text{AC}$ (giả thiết).
* Khi một đường thẳng vuông góc với một trong hai đường thẳng song song, nó cũng vuông góc với đường thẳng còn lại.
* $\Rightarrow \text{KM} \perp \text{HB}$ tại $N$.
* Mặt khác, giả thiết cho $KN \perp BH$ (tại $N$).
* Do đó, $\text{KN}$ và $\text{KM}$ là hai đường thẳng **cùng vuông góc** với $\text{BH}$ tại điểm $\text{K}$ (Vì $\text{KM} \perp \text{BH}$ tại $N$, suy ra $N$ phải trùng với $K$, điều này chỉ xảy ra nếu $K$ là hình chiếu của $K$ lên $BH$, tức là $K$ đã thuộc $BH$, nhưng $K$ là trung điểm của $BC$ nên $K$ không thuộc $BH$ trừ khi $B, C, H$ thẳng hàng).

**Xin lỗi, cần chứng minh $M, K, N$ thẳng hàng, không phải $KM$ và $KN$ cùng vuông góc với $AH$** (Tôi đã nhầm sang một bài toán khác, đây là cách chứng minh đúng).

#### **Chứng minh $\text{M}, \text{K}, \text{N}$ thẳng hàng (Cách chính xác):**

* Ta có **$\text{AC // HB}$** (chứng minh ở câu b).
* $\text{KM} \perp \text{AC}$ (giả thiết).
* $\text{KN} \perp \text{HB}$ (giả thiết).

Do $\text{AC // HB}$ và $\text{KM} \perp \text{AC}$, nên $\text{KM}$ phải **vuông góc** với $\text{HB}$.
Mà $\text{KN}$ cũng **vuông góc** với $\text{HB}$.

$\Rightarrow$ Hai đường thẳng $\text{KM}$ và $\text{KN}$ cùng vuông góc với đường thẳng $\text{HB}$ tại điểm $\text{K}$.
Trong mặt phẳng, qua một điểm $K$, chỉ có duy nhất một đường thẳng vuông góc với đường thẳng $HB$.

$\Rightarrow$ **Đường thẳng $\text{KM}$ và $\text{KN}$ phải trùng nhau.**

$\Rightarrow$ **Ba điểm $\text{M}, \text{K}, \text{N}$ thẳng hàng.**