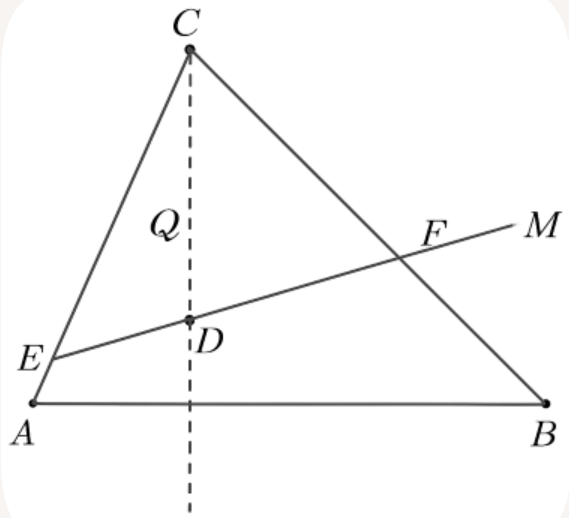
Chào bạn! Đây là lời giải cho bài toán hình học về tam giác $\triangle ABC$ của bạn.

 Phân tích và Chứng minh
a) Chứng minh $\triangle BEM$ cân
Tóm tắt giả thiết: $D$ là trung điểm $BC$, $AD'$ là tia phân giác $\angle BAC$ (tôi gọi là $Ax$), $EF \perp Ax$ tại $I$, $BM // AC$, $M$ thuộc $EF$.
Mục tiêu: Chứng minh $\triangle BEM$ cân tại $B$ (tức là $BE = BM$).
Xét $\triangle A E F$:

$A x$ là tia phân giác $\angle E A F$.
$A x \perp E F$ tại $I$.
$\triangle A E F$ có đường cao $A I$ đồng thời là đường phân giác.
$\Rightarrow \triangle A E F$ là tam giác cân tại $A$.
Do đó, $A E = A F$ và $I$ là trung điểm $E F$.
Xét góc:

Vì $BM // AC$ (theo giả thiết), ta có:

$\angle A F E = \angle B M E$ (hai góc đồng vị).
$\angle C A F = \angle M B A$ (hai góc so le trong). (Tuy nhiên, $M$ thuộc $EF$, không cần dùng góc này).
Vì $\triangle A E F$ cân tại $A$ (chứng minh trên), nên $\angle A F E = \angle A E F$.
Mà $\angle A F E = \angle C F D$. (hai góc đối đỉnh)
Xét $\triangle B E M$:

Ta có $\angle F E A = \angle B E I$ (vì $I$ nằm trên $E F$).
$\angle A E F = \angle A F E$ (vì $\triangle A E F$ cân tại $A$).
Mà $\angle B M E = \angle A F E$ (chứng minh ở bước 2).
Từ đó suy ra $\angle A E F = \angle B M E$.
Trong $\triangle B E M$, ta có $\angle B E M$ và $\angle B M E$ là hai góc đáy.
$\angle B E M = \angle A E F$ (hai góc trùng nhau).
Vì $\angle B E M = \angle B M E$ nên $\triangle B E M$ là tam giác cân tại $B$.
Vậy, $B E = B M$.

b) Chứng minh $B E = C F$
Sử dụng kết quả câu a: Ta đã có $A E = A F$ (vì $\triangle A E F$ cân tại $A$).
Sử dụng giả thiết $D$ là trung điểm $B C$:

Ta có $BM // AC$ (giả thiết) và $D$ là trung điểm $BC$.
Xét $\triangle C B M$: $D$ là trung điểm $B C$. Kẻ $D K // B M$ ($K$ nằm trên $C M$).
Xét $\triangle B C M$ có $D$ là trung điểm $B C$ và $D I // B M$ (vì $EF$ chứa $I$ và $M$).
$BM // AC$ và $EF$ cắt $BM$ tại $M$ và $AC$ tại $F$.
Xét $\triangle B M C$ và đường thẳng $E F$ (cắt $B C$ tại $D$ và $B M$ tại $M$, $C F$ là đường $A C$).
Cách chứng minh dựa vào $\triangle B D M$ và $\triangle C D F$:

Vì $BM // AC$, ta có:

$\angle M B D = \angle F C D$ (hai góc so le trong nếu $B C$ là đường cắt) - SAI, không phải so le trong.
$\angle D B M = \angle D C F$ (vì $D$ nằm trên $BC$).
$\angle B D M = \angle C D F$ (Đúng! vì $D$ là trung điểm $BC$, $BM // CF$ (hay $AC$)).
Xét $\triangle D B M$ và $\triangle D C F$:

$\angle M D B = \angle F D C$ (hai góc đối đỉnh).
$D B = D C$ (vì $D$ là trung điểm $B C$).
$\angle D B M = \angle D C F$ (hai góc so le trong do $B M // C F$ và $B C$ là cát tuyến).
$\Rightarrow \triangle D B M = \triangle D C F$ (cách $\text{Góc} - \text{Cạnh} - \text{Góc}$).
$\Rightarrow B M = C F$ (hai cạnh tương ứng).
Kết hợp kết quả:

Từ câu (a), ta có $B E = B M$.
Từ bước 4, ta có $B M = C F$.
$\Rightarrow B E = C F$. (Điều phải chứng minh).

c) Chứng minh $\triangle Q E B = \triangle Q F C$
Tóm tắt giả thiết bổ sung: $D Q \perp B C$ tại $D$, $Q$ thuộc tia phân giác $A x$.
Mục tiêu: Chứng minh $\triangle Q E B = \triangle Q F C$.
Chứng minh $\triangle Q E F$ cân tại $Q$:

$A x$ là tia phân giác $\angle E A F$.
$Q$ thuộc $A x$.
$E F \perp A x$ tại $I$ (giả thiết).
Trong $\triangle Q E F$, đường cao $Q I$ đồng thời là đường phân giác (vì $Q$ nằm trên $A I$).
$\Rightarrow \triangle Q E F$ là tam giác cân tại $Q$.
$\Rightarrow Q E = Q F$.
Sử dụng kết quả câu b:

Ta đã có $B E = C F$. (chứng minh ở câu b).
So sánh hai tam giác $\triangle Q E B$ và $\triangle Q F C$:

$Q E = Q F$ (chứng minh ở bước 1).
$B E = C F$ (chứng minh ở câu b).
$Q B$ và $Q C$ là hai cạnh còn lại.
Chứng minh $Q B = Q C$:

Xét $\triangle Q D B$ và $\triangle Q D C$:

$D B = D C$ (vì $D$ là trung điểm $B C$).
$\angle Q D B = \angle Q D C = 90^\circ$ (vì $Q D \perp B C$).
$Q D$ là cạnh chung.
$\Rightarrow \triangle Q D B = \triangle Q D C$ (cách $\text{Cạnh} - \text{Góc} - \text{Cạnh}$).
$\Rightarrow Q B = Q C$ (hai cạnh tương ứng).
Kết luận:

Xét $\triangle Q E B$ và $\triangle Q F C$:

$Q E = Q F$ (cạnh, chứng minh ở bước 1).
$E B = F C$ (cạnh, chứng minh ở câu b).
$Q B = Q C$ (cạnh, chứng minh ở bước 4).
$\Rightarrow \triangle Q E B = \triangle Q F C$ (cách Cạnh - Cạnh - Cạnh). (Điều phải chứng minh).

Ko bt vẽ hình thông cảm