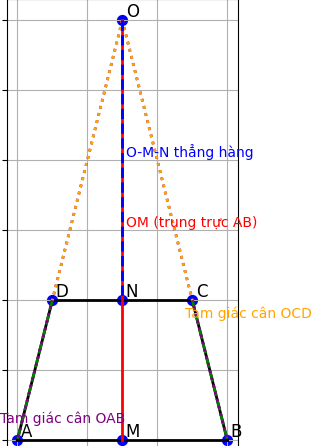
a) Chứng minh △OAB và △OCD là cân
- Trong hình thang AB // CD,góc C = góc D.
- Giao hai đường chéo mở rộng: DA ∩ CB = O.
- Xét tam giác OAB, có:
AB // CD nên các góc tại A và B bằng nhau khi tạo bởi đường chéo cắt hai đáy.
=> $\widehat{OAB}$ = $\widehat{OBA}$ (góc so le trong với đường chéo cắt hai đường song song).
Do đó OAB là tam giác cân tại O hoặc cân ở đáy AB (tùy cách xét).
- Xét tam giác OCD:
+ Tương tự, trong tam giác OCD, $\widehat{OCD}$ = $\widehat{ODC}$  vì $\hat{C}$ = $\hat{D}$ và CD là đáy hình thang.
Vậy tam giác OCD cũng cân tại O hoặc cân ở đáy CD.
=> △OAB và △OCD là tam giác cân.
b) Chứng minh OM là đường trung trực của AB
- Gọi M là trung điểm của AB.
- Trong tam giác cân OAB, trung tuyến từ đỉnh O (O đến M) đồng thời là đường trung trực của đáy AB.
=> OM ⊥ AB tại M, nghĩa là OM là đường trung trực của AB.
c) Chứng minh O, M, N thẳng hàng
Gọi N là trung điểm CD.
- Trong hình thang cân ABCD (vì $\hat{C} = \hat{D}$), đường trung bình của hình thang là đường nối trung điểm hai đáy, song song với hai đáy.
- Tam giác cân OAB và OCD cho thấy O nằm trên đường trung tuyến nối hai trung điểm đáy, tức O, M, N thẳng hàng.
=>  O, M, N thẳng hàng.

BÀI GIẢI CHI TIẾT 
Vẽ hình:
Vẽ đường thẳng song song AB với CD, lấy điểm D, C trên đường đó. Nối DA, CB. Giao điểm là O.
Lấy M là trung điểm AB, N là trung điểm CD. Nối O, M, N. 
a) Chứng minh △OCDtriangle cap O cap C cap D
△𝑂𝐶𝐷
và △OABtriangle cap O cap A cap B
△𝑂𝐴𝐵
là những tam giác cân: 
Xét △ODCtriangle cap O cap D cap C
△𝑂𝐷𝐶
:Ta có AB // CD (gt).
Do đó OAB̂=ODĈmodified cap O cap A cap B with hat above equals modified cap O cap D cap C with hat above
𝑂𝐴𝐵=𝑂𝐷𝐶
(so le trong) và OBÂ=OCD̂modified cap O cap B cap A with hat above equals modified cap O cap C cap D with hat above
𝑂𝐵𝐴=𝑂𝐶𝐷
(so le trong).
Vì ABCD là hình thang cân (do AB // CD và Ĉ=D̂cap C hat equals cap D hat
𝐶=𝐷
), ta có các góc ở đáy bằng nhau: DAB̂=CBÂmodified cap D cap A cap B with hat above equals modified cap C cap B cap A with hat above
𝐷𝐴𝐵=𝐶𝐵𝐴
(hay OAB̂=OBÂmodified cap O cap A cap B with hat above equals modified cap O cap B cap A with hat above
𝑂𝐴𝐵=𝑂𝐵𝐴
).
Suy ra OCD̂=ODĈmodified cap O cap C cap D with hat above equals modified cap O cap D cap C with hat above
𝑂𝐶𝐷=𝑂𝐷𝐶
.
Vậy △OCDtriangle cap O cap C cap D
△𝑂𝐶𝐷
cân tại O (đpcm).

Xét △OABtriangle cap O cap A cap B
△𝑂𝐴𝐵
:Từ OAB̂=OBÂmodified cap O cap A cap B with hat above equals modified cap O cap B cap A with hat above
𝑂𝐴𝐵=𝑂𝐵𝐴
(chứng minh trên), ta có △OABtriangle cap O cap A cap B
△𝑂𝐴𝐵
cân tại O (đpcm). 

b) Chứng minh đường thẳng OM là đường trung trực của đoạn thẳng AB: 
Xét △OABtriangle cap O cap A cap B
△𝑂𝐴𝐵
cân tại O:M là trung điểm AB (gt).
Trong tam giác cân, đường trung tuyến ứng với cạnh đáy đồng thời là đường cao, đường phân giác.
Vậy OM ⟂⟂
⟂
AB (OM là đường cao).

Kết luận: Đường thẳng OM vừa đi qua trung điểm M của AB, vừa vuông góc với AB, nên OM là đường trung trực của AB (đpcm). 

c) Chứng minh ba điểm O, M, N thẳng hàng: 
Xét △ODCtriangle cap O cap D cap C
△𝑂𝐷𝐶
cân tại O:N là trung điểm CD (gt).
ON là đường trung tuyến ứng với cạnh đáy CD.
Vậy ON ⟂⟂
⟂
CD (ON là đường cao).

Xét đường thẳng MN:MN đi qua trung điểm M của AB (AB // CD).
MN đi qua trung điểm N của CD (AB // CD).
Trong hình thang cân, đường nối trung điểm hai đáy thì vuông góc với hai đáy. Suy ra MN ⟂⟂
⟂
AB và MN ⟂⟂
⟂
CD.

Kết luận:Cả OM và ON đều vuông góc với AB (hoặc CD) tại M (hoặc N).
Mặt khác, O, M, N đều nằm trên đường thẳng đi qua trung điểm hai đáy AB và CD (hoặc là đường trung bình của hình thang nếu xét theo cạnh bên, nhưng ở đây liên quan giao điểm hai cạnh bên).
Vì qua một điểm (M) chỉ có một đường thẳng vuông góc với một đường thẳng (AB) (hoặc qua điểm N và vuông góc CD) và O, M, N nằm trên đường thẳng này (do tính đối xứng của hì

 Chứng minh a) Chứng minh hai tam giác OCD và OAB là những tam giác cân 1. Tam giác OCD

• Ta có hình thang ABCD với ∠C=∠D (giả thiết).

• Xét tam giác OCD, vì nó có ∠D=∠C, nên tam giác OCD là tam giác cân tại O.

• Suy ra: OD=OC.

2. Tam giác OAB

• Vì AB//CD (tính chất hình thang), ta có các cặp góc đồng vị bằng nhau:

  • ∠OAB=∠ODC

  • ∠OBA=∠OCD

• Mà ∠ODC=∠OCD (do △OCD cân).

• Suy ra, ∠OAB=∠OBA.

• Xét tam giác OAB, vì nó có hai góc ở đáy bằng nhau, nên tam giác OAB là tam giác cân tại O.

• Suy ra: OA=OB.

b) Chứng minh đường thẳng OM là đường trung trực của đoạn thẳng AB

• Tóm tắt: Ta đã có △OAB cân tại O (chứng minh ở câu a).

• M là trung điểm của cạnh đáy AB (giả thiết).

• Trong tam giác cân, đường trung tuyến xuất phát từ đỉnh O (đoạn OM) đồng thời là đường cao.

• Do đó, OM⊥AB.

• Kết luận: Đường thẳng OM đi qua trung điểm M và vuông góc với AB tại M, nên OM là đường trung trực của đoạn thẳng AB.

c) Chứng minh ba điểm O,M,N thẳng hàng

• 1. Xét ON

  • △OCD cân tại O (chứng minh ở câu a).

  • N là trung điểm của cạnh đáy CD (giả thiết).

  • Trong tam giác cân OCD, đường trung tuyến ON cũng là đường cao.

  • Suy ra, ON⊥CD.

• 2. Xét vị trí của OM và ON

  • Ta có OM⊥AB (tính chất đường trung trực của AB).

  • Ta có ON⊥CD (tính chất đường trung tuyến kiêm đường cao của △OCD).

  • Vì AB//CD (giả thiết), mà OM và ON đều vuông góc với hai đường thẳng song song này.

  • Do đó, OM và ON phải cùng nằm trên một đường thẳng (vì cả hai đều là đường thẳng duy nhất đi qua O và vuông góc với AB và CD).

• Kết luận: Ba điểm O,M,N thẳng hàng.