Cho tứ diện ABCD có G là trọng tâm, tam giác BCD biết mặt phẳng A chứa BG và song song với AC. Tìm giao điểm K của AD và mặt phẳng A
Quảng cáo
3 câu trả lời 547
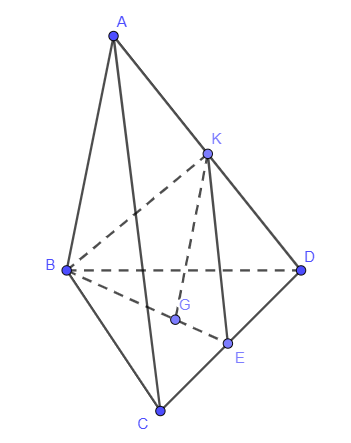
Gọi E là trung điểm DC
Trong (ACD) kẻ EK // AC
=> Mặt phẳng (A) chính là (BGK)
=> AD (BGE) = K, K là trung điểm AD
Để tìm giao điểm
Kcap K
𝐾
của đường thẳng ADcap A cap D
𝐴𝐷
và mặt phẳng (a)open paren a close paren
(𝑎)
chứa BGcap B cap G
𝐵𝐺
và song song với ACcap A cap C
𝐴𝐶
, ta tìm giao tuyến của (a)open paren a close paren
(𝑎)
với mặt phẳng (ACD)open paren cap A cap C cap D close paren
(𝐴𝐶𝐷)
. Vì (a)∥(ACD)open paren a close paren is parallel to open paren cap A cap C cap D close paren
(𝑎)∥(𝐴𝐶𝐷)
, nên giao tuyến này sẽ song song với ACcap A cap C
𝐴𝐶
. Điểm Kcap K
𝐾
sẽ là giao điểm của ADcap A cap D
𝐴𝐷
với giao tuyến này.
Xác định mặt phẳng chứa BGcap B cap G
𝐵𝐺
song song với ACcap A cap C
𝐴𝐶
:Gọi mặt phẳng (a)open paren a close paren
(𝑎)
là mặt phẳng cần tìm.
Ta có BG⊂(a)cap B cap G is a subset of open paren a close paren
𝐵𝐺⊂(𝑎)
và (a)∥ACopen paren a close paren is parallel to cap A cap C
(𝑎)∥𝐴𝐶
.
Tìm giao tuyến của mặt phẳng (a)open paren a close paren
(𝑎)
với mặt phẳng (BCD)open paren cap B cap C cap D close paren
(𝐵𝐶𝐷)
:Vì BGcap B cap G
𝐵𝐺
nằm trong mặt phẳng (a)open paren a close paren
(𝑎)
và Gcap G
𝐺
là trọng tâm tam giác BCDcap B cap C cap D
𝐵𝐶𝐷
, nên BGcap B cap G
𝐵𝐺
cũng nằm trong mặt phẳng (BCD)open paren cap B cap C cap D close paren
(𝐵𝐶𝐷)
.
Giao tuyến của mặt phẳng (a)open paren a close paren
(𝑎)
và mặt phẳng (BCD)open paren cap B cap C cap D close paren
(𝐵𝐶𝐷)
chính là đường thẳng BGcap B cap G
𝐵𝐺
.
Tìm giao tuyến của mặt phẳng (a)open paren a close paren
(𝑎)
với mặt phẳng (ACD)open paren cap A cap C cap D close paren
(𝐴𝐶𝐷)
:Gọi giao tuyến của mặt phẳng (a)open paren a close paren
(𝑎)
với mặt phẳng (ACD)open paren cap A cap C cap D close paren
(𝐴𝐶𝐷)
là đường thẳng dd
𝑑
.
Ta có (a)∥ACopen paren a close paren is parallel to cap A cap C
(𝑎)∥𝐴𝐶
. Vì ACcap A cap C
𝐴𝐶
nằm trong mặt phẳng (ACD)open paren cap A cap C cap D close paren
(𝐴𝐶𝐷)
, nên giao tuyến dd
𝑑
cũng phải song song với ACcap A cap C
𝐴𝐶
.
Do đó, d∥ACd is parallel to cap A cap C
𝑑∥𝐴𝐶
và d⊂(ACD)d is a subset of open paren cap A cap C cap D close paren
𝑑⊂(𝐴𝐶𝐷)
.
Tìm điểm Kcap K
𝐾
:Điểm Kcap K
𝐾
là giao điểm của ADcap A cap D
𝐴𝐷
và mặt phẳng (a)open paren a close paren
(𝑎)
, tức là K=AD∩(a)cap K equals cap A cap D intersection open paren a close paren
𝐾=𝐴𝐷∩(𝑎)
.
Vì Kcap K
𝐾
nằm trên ADcap A cap D
𝐴𝐷
, nên Kcap K
𝐾
cũng nằm trên mặt phẳng (ACD)open paren cap A cap C cap D close paren
(𝐴𝐶𝐷)
.
Vì Kcap K
𝐾
nằm trên mặt phẳng (a)open paren a close paren
(𝑎)
, nên Kcap K
𝐾
cũng nằm trên giao tuyến dd
𝑑
của (a)open paren a close paren
(𝑎)
và (ACD)open paren cap A cap C cap D close paren
(𝐴𝐶𝐷)
.
Do đó, Kcap K
𝐾
là giao điểm của ADcap A cap D
𝐴𝐷
và đường thẳng dd
𝑑
(giao tuyến của (a)open paren a close paren
(𝑎)
và (ACD)open paren cap A cap C cap D close paren
(𝐴𝐶𝐷)
).
Kết luận:Ta kẻ đường thẳng dd
𝑑
qua Bcap B
𝐵
song song với ACcap A cap C
𝐴𝐶
.
Tìm giao điểm Icap I
𝐼
của dd
𝑑
và CDcap C cap D
𝐶𝐷
.
Tìm giao điểm Jcap J
𝐽
của AIcap A cap I
𝐴𝐼
với ADcap A cap D
𝐴𝐷
. Điểm Jcap J
𝐽
chính là Kcap K
𝐾
..
Để tìm giao điểm
Kcap K
𝐾
của đường thẳng ADcap A cap D
𝐴𝐷
và mặt phẳng (a)open paren a close paren
(𝑎)
chứa BGcap B cap G
𝐵𝐺
và song song với ACcap A cap C
𝐴𝐶
, ta tìm giao tuyến của (a)open paren a close paren
(𝑎)
với mặt phẳng (ACD)open paren cap A cap C cap D close paren
(𝐴𝐶𝐷)
. Vì (a)∥(ACD)open paren a close paren is parallel to open paren cap A cap C cap D close paren
(𝑎)∥(𝐴𝐶𝐷)
, nên giao tuyến này sẽ song song với ACcap A cap C
𝐴𝐶
. Điểm Kcap K
𝐾
sẽ là giao điểm của ADcap A cap D
𝐴𝐷
với giao tuyến này.
Xác định mặt phẳng chứa BGcap B cap G
𝐵𝐺
song song với ACcap A cap C
𝐴𝐶
:Gọi mặt phẳng (a)open paren a close paren
(𝑎)
là mặt phẳng cần tìm.
Ta có BG⊂(a)cap B cap G is a subset of open paren a close paren
𝐵𝐺⊂(𝑎)
và (a)∥ACopen paren a close paren is parallel to cap A cap C
(𝑎)∥𝐴𝐶
.
Tìm giao tuyến của mặt phẳng (a)open paren a close paren
(𝑎)
với mặt phẳng (BCD)open paren cap B cap C cap D close paren
(𝐵𝐶𝐷)
:Vì BGcap B cap G
𝐵𝐺
nằm trong mặt phẳng (a)open paren a close paren
(𝑎)
và Gcap G
𝐺
là trọng tâm tam giác BCDcap B cap C cap D
𝐵𝐶𝐷
, nên BGcap B cap G
𝐵𝐺
cũng nằm trong mặt phẳng (BCD)open paren cap B cap C cap D close paren
(𝐵𝐶𝐷)
.
Giao tuyến của mặt phẳng (a)open paren a close paren
(𝑎)
và mặt phẳng (BCD)open paren cap B cap C cap D close paren
(𝐵𝐶𝐷)
chính là đường thẳng BGcap B cap G
𝐵𝐺
.
Tìm giao tuyến của mặt phẳng (a)open paren a close paren
(𝑎)
với mặt phẳng (ACD)open paren cap A cap C cap D close paren
(𝐴𝐶𝐷)
:Gọi giao tuyến của mặt phẳng (a)open paren a close paren
(𝑎)
với mặt phẳng (ACD)open paren cap A cap C cap D close paren
(𝐴𝐶𝐷)
là đường thẳng dd
𝑑
.
Ta có (a)∥ACopen paren a close paren is parallel to cap A cap C
(𝑎)∥𝐴𝐶
. Vì ACcap A cap C
𝐴𝐶
nằm trong mặt phẳng (ACD)open paren cap A cap C cap D close paren
(𝐴𝐶𝐷)
, nên giao tuyến dd
𝑑
cũng phải song song với ACcap A cap C
𝐴𝐶
.
Do đó, d∥ACd is parallel to cap A cap C
𝑑∥𝐴𝐶
và d⊂(ACD)d is a subset of open paren cap A cap C cap D close paren
𝑑⊂(𝐴𝐶𝐷)
.
Tìm điểm Kcap K
𝐾
:Điểm Kcap K
𝐾
là giao điểm của ADcap A cap D
𝐴𝐷
và mặt phẳng (a)open paren a close paren
(𝑎)
, tức là K=AD∩(a)cap K equals cap A cap D intersection open paren a close paren
𝐾=𝐴𝐷∩(𝑎)
.
Vì Kcap K
𝐾
nằm trên ADcap A cap D
𝐴𝐷
, nên Kcap K
𝐾
cũng nằm trên mặt phẳng (ACD)open paren cap A cap C cap D close paren
(𝐴𝐶𝐷)
.
Vì Kcap K
𝐾
nằm trên mặt phẳng (a)open paren a close paren
(𝑎)
, nên Kcap K
𝐾
cũng nằm trên giao tuyến dd
𝑑
của (a)open paren a close paren
(𝑎)
và (ACD)open paren cap A cap C cap D close paren
(𝐴𝐶𝐷)
.
Do đó, Kcap K
𝐾
là giao điểm của ADcap A cap D
𝐴𝐷
và đường thẳng dd
𝑑
(giao tuyến của (a)open paren a close paren
(𝑎)
và (ACD)open paren cap A cap C cap D close paren
(𝐴𝐶𝐷)
).
Kết luận:Ta kẻ đường thẳng dd
𝑑
qua Bcap B
𝐵
song song với ACcap A cap C
𝐴𝐶
.
Tìm giao điểm Icap I
𝐼
của dd
𝑑
và CDcap C cap D
𝐶𝐷
.
Tìm giao điểm Jcap J
𝐽
của AIcap A cap I
𝐴𝐼
với ADcap A cap D
𝐴𝐷
. Điểm Jcap J
𝐽
chính là Kcap K
𝐾
..
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
135338
Đã trả lời bởi chuyên gia
135338 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
76535
Đã trả lời bởi chuyên gia
76535 -
 Đã trả lời bởi chuyên gia
72150
Đã trả lời bởi chuyên gia
72150 -
 Đã trả lời bởi chuyên gia
47764
Đã trả lời bởi chuyên gia
47764


