Question

Đã trả lời bởi chuyên gia

Answer 1

`a,` Xét tứ giác `ECDF` có :

`FC //ED `

` FC = ED = \frac{1}{2} AD`

Suy ra `AB = BE =EF = EC`

Suy ra `CDFE` là hình thoi

`b,`Tứ giác `ABED` là hình thang cân vì `BE // AD`

`\hat{BAD} = \hat{ADE} = 60^0`

Answer 2

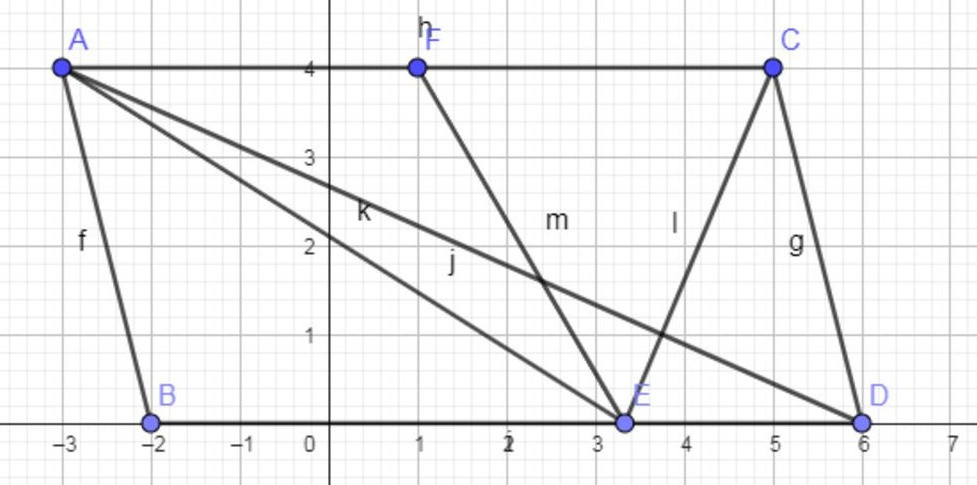
a.Giải:

Ta có:

* ABCD là **hình bình hành** ⇒ **AD ∥ BC** và **AB ∥ CD**, đồng thời **AB = CD**, **BC = AD**.

* E là **trung điểm của BC** ⇒ **BE = EC = ½ BC**.

* F là **trung điểm của AD** ⇒ **AF = FD = ½ AD**.

Do trong hình bình hành, **AD = BC**, ta suy ra:
[
EC = \frac{1}{2}BC = \frac{1}{2}AD = FD.
]

Vậy ta có:
[
EC = FD.
]

Tiếp theo xét các đoE nằm trên BCF nằm trên AD**, mà BC ∥ AD → **EF ∥ BD** (đường nối trung điểm trong hai cạnh song song).C và D nằm trên CD, mà CD ∥ AB → CD ∥ AB.

Tuy nhiên, quan trọng nhất là ta chứng minh được hai cặp cạnh đối của tứ giác ECDF bằng nhau:

Ta đã có EC = FD.
Tương tự:

CE = ½ BC
DF = ½ AD
mà BC = AD → CE = DF (đã chứng minh trên).
Ta cũng có:

CD là cạnh của hình bình hành.
E và F là trung điểm, nên
EF = \frac{1}{2}CD.
Tương tự:
CD = 2 \cdot EF.]
Mà C và D chính là hai đỉnh kề của hình thoi cần xét.

Từ đó suy ra:EC = FD \quad \text{và} \quad CF = DE.]

Tứ giác có hai cặp cạnh kề bằng nhau ⇒ ECDF là hình thoi.

Kết luận:

Tứ giác ECDF là hình thoi vì nó có EC = FD và CF = DE, tức là bốn cạnh bằng nhau.

...Xem thêm

Answer 3