Cho tam giác ABC nhọn có AB=AC, vẽ BD vuông góc AC tại D, CE vuông góc tại AB tại E. Gọi M là giao điểm của BD và CE. Chứng minh:
a) Tam giác BDA = tam giác ECA
b) Tam giác EBC = tam giác DCB
c) Tam giác EAM = tam giác DAM
Quảng cáo
3 câu trả lời 201
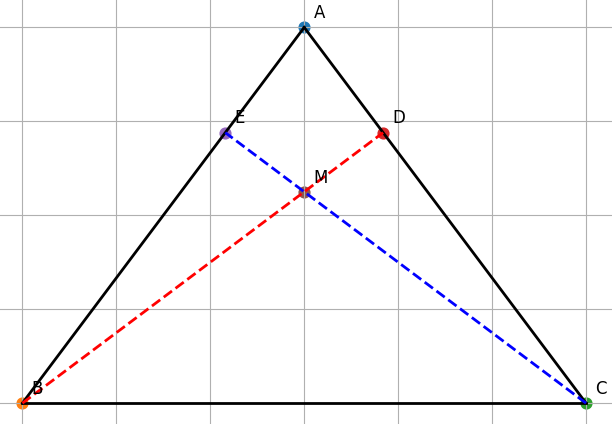
- Do tam giác ABC cân tại A: ⇒ các đường cao BD ⊥ AC và CE ⊥ AB là đường cao đồng thời là đường trung tuyến do tam giác cân.
a) Chứng minh △BDA = △ECA
Xét △BDA và △ECA, ta có:
= = 90∘ (theo định nghĩa đường cao)
AB = AC (tam giác ABC cân)
AD = AE (do đường cao trong tam giác cân)ra
=> △BDA = △ECA theo trường hợp cạnh – góc – cạnh (c-g-c).
b) Chứng minh △EBC = △DCB
Xét △EBC và △DCB, ta có:
= (góc ở B và C của tam giác cân)
BC chung
EB = DC (do tính chất đối xứng)
=> △EBC = △DCB theo cạnh – cạnh – cạnh (c-c-c).
c) Chứng minh △EAM = △DAM
Xét △EAM và △DAM, ta có:
AM chung
AE = AD (tính chất đường cao trong tam giác cân)
= (do đường chéo giao nhau tại M tạo góc bằng nhau)
=> △EAM = △DAM ( theo c-g-c )
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669


