Quảng cáo
3 câu trả lời 91
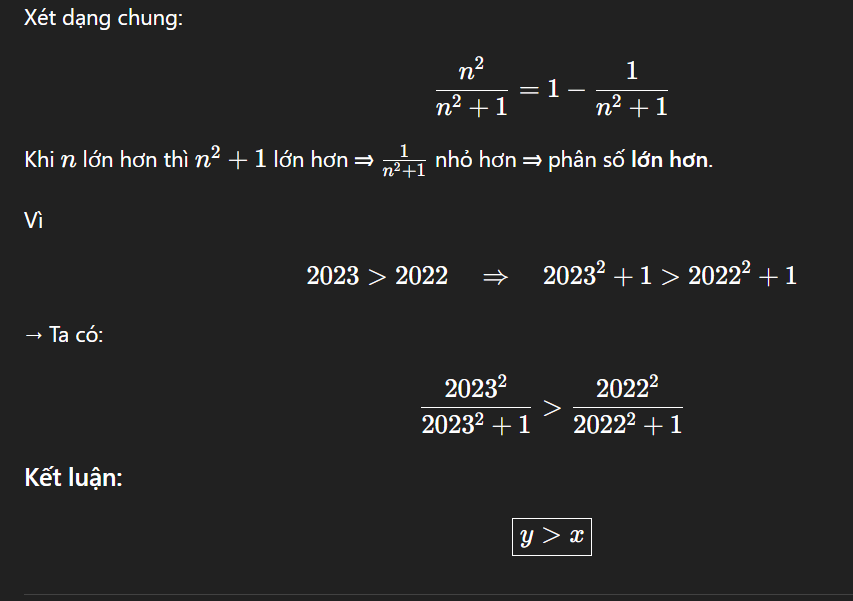
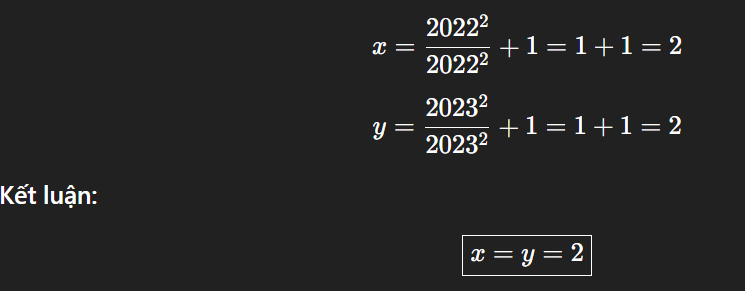
Chúng ta có:
\[
x = \frac{2022^2}{2022^2 + 1}
\]
và
\[
y = \frac{2023^2}{2023^2 + 1}
\]
Bây giờ, hãy so sánh \(x\) và \(y\).
---
\[
\frac{A}{A + 1}
\]
với \(A > 0\).
Vì vậy, ta có thể so sánh giá trị của \(\frac{A}{A+1}\) khi \(A\) thay đổi.
Xét hàm:
\[
f(A) = \frac{A}{A+1}
\]
khi \(A > 0\).
Hàm này tăng khi \(A\) tăng, vì:
\[
f'(A) = \frac{(A+1) - A}{(A+1)^2} = \frac{1}{(A+1)^2} > 0
\]
do đó, \(f(A)\) là hàm tăng trên \(\mathbb{R}^+\).
- \(A_1 = 2022^2\)
- \(A_2 = 2023^2\)
Ta thấy rõ:
\[
A_2 > A_1
\]
bởi vì:
\[
2023^2 = (2022 + 1)^2 = 2022^2 + 2 \times 2022 + 1 > 2022^2
\]
---
Vì hàm \(f(A)\) là hàm tăng và \(A_2 > A_1\), nên:
\[
f(A_2) > f(A_1)
\]
tức là:
\[
y = \frac{2023^2}{2023^2 + 1} > \frac{2022^2}{2022^2 + 1} = x
\]
\[
\boxed{
\text{Ta có } y > x
}
\]
Quảng cáo
Bạn hỏi - Chuyên gia trả lời
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
Đã trả lời bởi chuyên gia
81713 -
Đã trả lời bởi chuyên gia
59651
-
Đã trả lời bởi chuyên gia
39669
-
보고 싶어요
2140 điểm
-
😗
900 điểm
-
🌷김은✨
590 điểm
-
`color{blue}text{HuyTùng☢`
575 điểm
-
𝘳𝘺𝘯.𝘭𝘦𝘦ッ
540 điểm
-
jgdmaX
345 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
300 điểm
-
Kiều Anh 295 điểm
-
돈이없다 💸😭
260 điểm
-
༘⋆nhỏ nho𓏲ּ𝄢
225 điểm
-
devestro
210 điểm
-
너 없는 파리
190 điểm
-
Ben 23K
180 điểm
-
누가 고철을 팔고 싶어할까요🗑️🗑️
160 điểm
-
Hai Trieu
150 điểm
Rút gọn
Bài viết mới nhất Lớp 7
-
2 năm trước4944
