Quảng cáo
3 câu trả lời 266
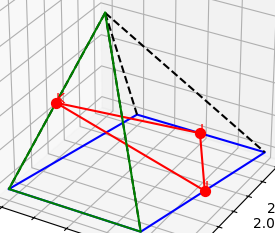
Ta có:
I là trung điểm của BC, nên I ∈ BC.
J là trung điểm của CD, nên J ∈ C.
K là trung điểm của SA, nên K ∈ SA.
- Xét hai mặt phẳng (IJK) và (SAB):
+ Mặt phẳng (IJK) chứa ba điểm I, J, K.
+ Mặt phẳng (SAB) chứa ba điểm S, A, B.
- Giao tuyến của hai mặt phẳng:
+ Vì K nằm trên đoạn SA nên K ∈ (SAB).
+ Điểm I nằm trên BC, còn điểm J nằm trên CD, hai đoạn thẳng này thuộc đáy ABCD, không thuộc mặt phẳng (SAB) vì đáy và mặt phẳng (SAB) chỉ chung đường thẳng AB.
- Giao điểm G của đoạn thẳng IJ với đoạn AB:
+ Cả I và J đều nằm trên đáy ABCD, do đó I, J, A, B cùng nằm trong mặt phẳng đáy.
+ Đường thẳng AB thuộc mặt phẳng (SAB).
+ Giao điểm G của đoạn IJ với đoạn AB nằm trên cả hai mặt phẳng (IJK) và (SAB).
=> Giao tuyến của hai mặt phẳng (IJK) và (SAB) là đường thẳng đi qua hai điểm K và G.
=> KG = (IJK) ∩ (SAB)
Bạn đang muốn tìm giao tuyến của hai mặt phẳng \((IJK)\) và \((SAB)\) trong hình chóp \(S.ABCD\), trong đó đáy \(ABCD\) là hình bình hành, và các điểm \(I, J, K\) lần lượt là trung điểm của các đoạn \(BC\), \(CD\), và \(SA\).
---
### Bước 1: Phân tích dữ liệu đề bài
- \(ABCD\): hình bình hành
- \(S\): đỉnh chóp
- \(I\): trung điểm của \(BC\)
- \(J\): trung điểm của \(CD\)
- \(K\): trung điểm của \(SA\)
---
### Bước 2: Đặt hệ toạ độ
Để dễ dàng tính toán, ta chọn hệ toạ độ như sau:
- \(A = (0,0,0)\)
- \(B = (a,0,0)\)
- \(D = (0,b,0)\)
- \(C = B + D = (a, b, 0)\)
- \(S = (0,0,h)\)
Trong đó:
- \(a, b, h > 0\)
---
### Bước 3: Tính các điểm trung điểm
- \(I\) là trung điểm của \(BC\):
\[
B = (a, 0, 0), \quad C = (a, b, 0)
\]
\[
I = \left( \frac{a + a}{2}, \frac{0 + b}{2}, 0 \right) = (a, \frac{b}{2}, 0)
\]
- \(J\) là trung điểm của \(CD\):
\[
C = (a, b, 0), \quad D = (0, b, 0)
\]
\[
J = \left( \frac{a + 0}{2}, \frac{b + b}{2}, 0 \right) = \left( \frac{a}{2}, b, 0 \right)
\]
- \(K\) là trung điểm của \(SA\):
\[
S = (0, 0, h), \quad A = (0, 0, 0)
\]
\[
K = \left( \frac{0 + 0}{2}, \frac{0 + 0}{2}, \frac{h + 0}{2} \right) = (0, 0, \frac{h}{2})
\]
---
### Bước 4: Viết các phương trình mặt phẳng
#### Mặt phẳng \((IJK)\):
- Ba điểm:
\[
I = (a, \frac{b}{2}, 0)
\]
\[
J = \left( \frac{a}{2}, b, 0 \right)
\]
\[
K = (0, 0, \frac{h}{2})
\]
- Tìm vectơ:
\[
\vec{IJ} = J - I = \left( \frac{a}{2} - a, \quad b - \frac{b}{2}, \quad 0 - 0 \right) = \left( -\frac{a}{2}, \frac{b}{2}, 0 \right)
\]
\[
\vec{IK} = K - I = (0 - a, \quad 0 - \frac{b}{2}, \quad \frac{h}{2} - 0) = (-a, -\frac{b}{2}, \frac{h}{2})
\]
- Vécơ pháp của mặt phẳng \((IJK)\):
\[
\vec{n}_{IJK} = \vec{IJ} \times \vec{IK}
\]
Tính tích:
\[
\vec{n}_{IJK} =
\begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
-\frac{a}{2} & \frac{b}{2} & 0 \\
- a & -\frac{b}{2} & \frac{h}{2}
\end{vmatrix}
\]
Tính theo từng thành phần:
- Thành phần \(x\):
\[
\left( \frac{b}{2} \times \frac{h}{2} - 0 \times -\frac{b}{2} \right) = \frac{b h}{4}
\]
- Thành phần \(y\):
\[
- \left( -\frac{a}{2} \times \frac{h}{2} - 0 \times -a \right) = - \left( -\frac{a h}{4} \right) = \frac{a h}{4}
\]
- Thành phần \(z\):
\[
-\frac{a}{2} \times -\frac{b}{2} - \frac{b}{2} \times -a = \frac{a b}{4} + \frac{a b}{2} = \frac{a b}{4} + \frac{2 a b}{4} = \frac{3 a b}{4}
\]
Vậy:
\[
\vec{n}_{IJK} = \left( \frac{b h}{4}, \frac{a h}{4}, \frac{3 a b}{4} \right)
\]
Phương trình mặt phẳng \((IJK)\):
\[
\frac{b h}{4}(x - a) + \frac{a h}{4}(y - \frac{b}{2}) + \frac{3 a b}{4}(z - 0) = 0
\]
---
### Bước 5: Tìm giao tuyến của \((IJK)\) và \((SAB)\)
- **Mặt phẳng \((SAB)\):**
Điểm:
\[
S = (0, 0, h), \quad A = (0, 0, 0), \quad B = (a, 0, 0)
\]
- Vécơ pháp:
\[
\vec{AB} = (a, 0, 0), \quad \vec{AS} = (0, 0, h)
\]
- Phương trình mặt phẳng \((SAB)\):
\[
\text{Vécơ pháp} = \vec{AB} \times \vec{AS} =
\begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
a & 0 & 0 \\
0 & 0 & h
\end{vmatrix}
= (0 \times h - 0 \times 0)\mathbf{i} - (a \times h - 0 \times 0)\mathbf{j} + (a \times 0 - 0 \times 0)\mathbf{k} = (0, -a h, 0)
\]
- Phương trình mặt phẳng \((SAB)\):
\[
0 (x - 0) - a h (y - 0) + 0 (z - 0) = 0 \Rightarrow -a h y = 0 \Rightarrow y = 0
\]
---
### **Kết luận:**
- Mặt phẳng \((SAB)\): \( y = 0 \)
- Giao tuyến của \((IJK)\) và \((SAB)\):
Điều kiện để điểm thuộc cả hai mặt phẳng:
\[
\boxed{ y = 0 }
\]
Thay \( y=0 \) vào phương trình mặt phẳng \((IJK)\):
\[
\frac{b h}{4}(x - a) + \frac{a h}{4}(0 - \frac{b}{2}) + \frac{3 a b}{4}(z - 0) = 0
\]
Rút gọn:
\[
\frac{b h}{4}(x - a) - \frac{a h b}{8} + \frac{3 a b}{4} z = 0
\]
Chia cả phương trình cho \(\frac{b}{4}\):
\[
h (x - a) - \frac{a h}{2} + 3 a z = 0
\]
\[
h x - h a - \frac{a h}{2} + 3 a z = 0
\]
\[
h x + 3 a z = h a + \frac{a h}{2} = \frac{2 h a + h a}{2} = \frac{3 h a}{2}
\]
---
### **Giao tuyến:**
\[
\boxed{
\begin{cases}
y = 0 \\
h x + 3 a z = \frac{3 h a}{2}
\end{cases}
}
\]
Hoặc:
\[
h x + 3 a z = \frac{3 h a}{2}
\]
Điều này mô tả một đường thẳng nằm trong mặt phẳng \( y=0 \), có phương trình:
\[
\text{Giao tuyến là đường thẳng} \quad \text{trên } y=0, \text{thỏa mãn } h x + 3 a z = \frac{3 h a}{2}
\]
---
### **Tóm lại:**
**Giao tuyến của hai mặt phẳng \((IJK)\) và \((SAB)\) là đường thẳng nằm trong mặt phẳng \( y=0 \), có phương trình:**
\[
h x + 3 a z = \frac{3 h a}{2}
\]
---
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
134838
Đã trả lời bởi chuyên gia
134838 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
75920
Đã trả lời bởi chuyên gia
75920 -
 Đã trả lời bởi chuyên gia
71641
Đã trả lời bởi chuyên gia
71641 -
 Đã trả lời bởi chuyên gia
47575
Đã trả lời bởi chuyên gia
47575


