Bạn muốn xét sự biến thiên và vẽ đồ thị của hàm số:

\[
y = -x^2 + 4x + 5
\]

---

### Bước 1: Xác định dạng của hàm số

Hàm số đã ở dạng chuẩn của một hàm bậc hai:

\[
y = ax^2 + bx + c
\]

Ở đây: \( a = -1 \), \( b = 4 \), \( c = 5 \).

### Bước 2: Xét sự biến thiên

- Do \( a = -1 < 0 \), đồ thị là một parabola hướng xuống.
- Tìm đỉnh của parabola, vì đó là điểm cực trị (điểm cực đại).

### Bước 3: Tìm hoành độ đỉnh \( x_{đ} \)

Công thức:

\[
x_{đ} = -\frac{b}{2a} = -\frac{4}{2 \times (-1)} = -\frac{4}{-2} = 2
\]

### Bước 4: Tính \( y_{đ} \) tại \( x = 2 \)

\[
y_{đ} = - (2)^2 + 4 \times 2 + 5 = -4 + 8 + 5 = 9
\]

### Kết quả:

- Đỉnh của parabola là \( (2, 9) \).
- Đồ thị mở xuống (vì \( a < 0 \)).
- Đồ thị có dạng hình như một "nước rút" với đỉnh tại \( (2, 9) \).

---

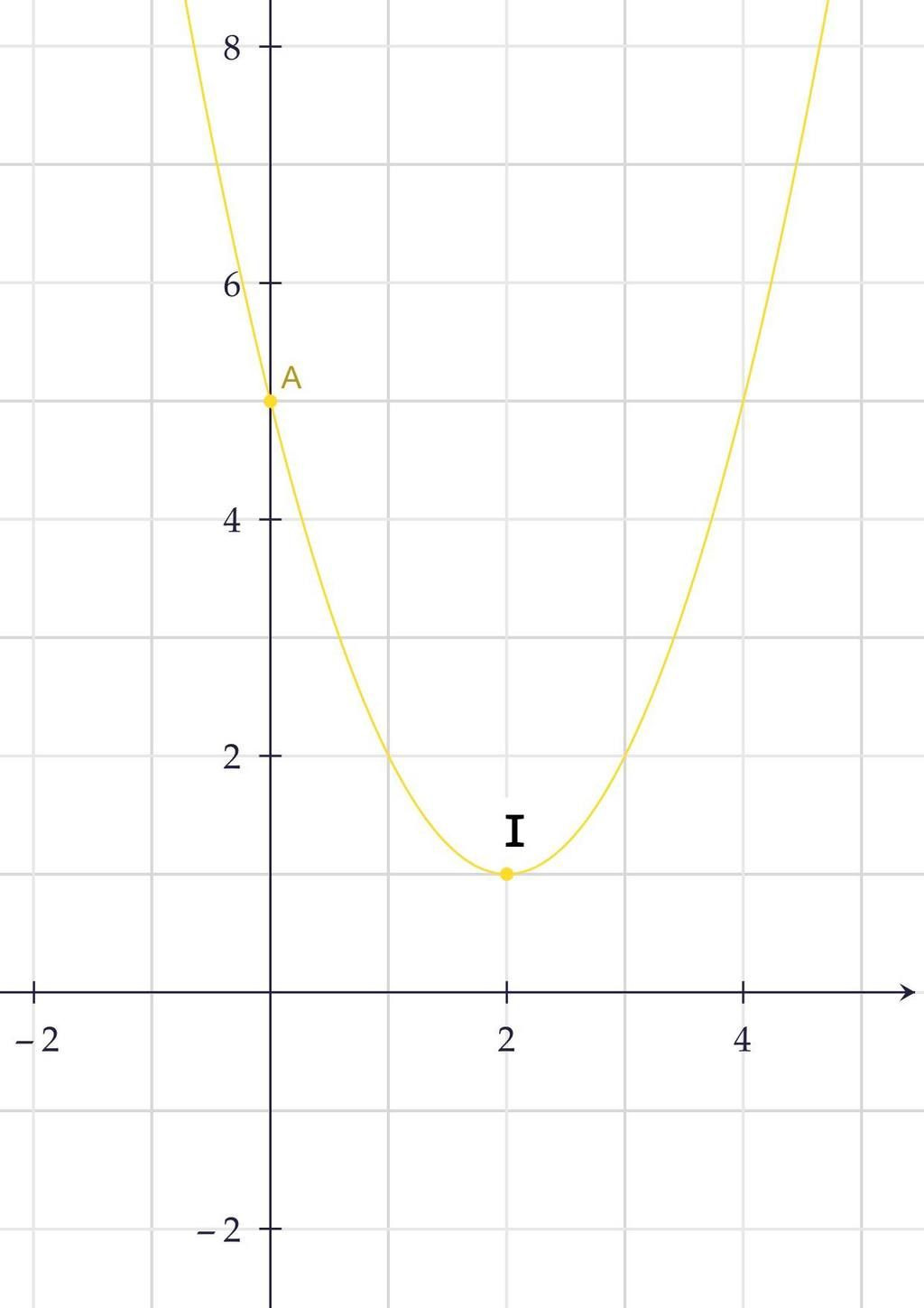
### Bước 5: Vẽ đồ thị

Bạn có thể vẽ đồ thị bằng cách:

- Đánh dấu đỉnh tại \( (2, 9) \).
- Tính giá trị \( y \) tại các giá trị của \( x \) xung quanh đỉnh để xác định dạng đồ thị.
- Đồ thị sẽ có dạng parabola mở xuống, đi qua các điểm:

\[
x = 0: y = -0 + 0 + 5 = 5
\]
\[
x = 4: y = -16 + 16 + 5 = 5
\]

Và các điểm khác để có hình dạng chính xác.

---