Quảng cáo
3 câu trả lời 126
Dưới đây là chứng minh cơ bản cho các công thức lượng giác bạn hỏi, dựa trên tam giác vuông và định nghĩa lượng giác:



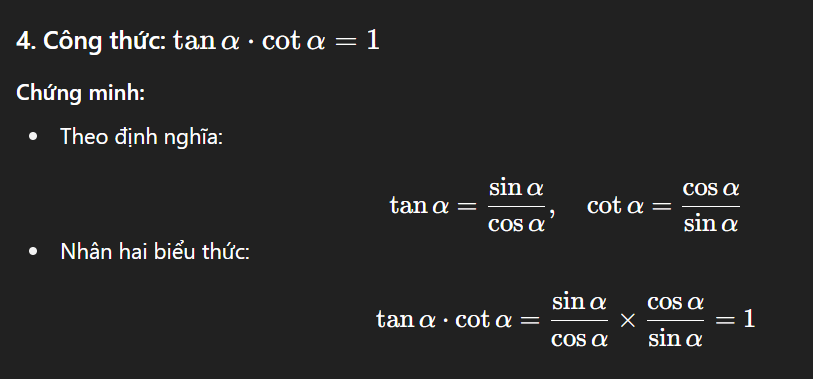
.......
miu
· 3 tháng trước
spam?
🅿🅷á🆃
· 3 tháng trước
ýe
miu
· 3 tháng trước
mất acc đấy
🅿🅷á🆃
· 3 tháng trước
ko phải lo
miu
· 3 tháng trước
-_-
🅿🅷á🆃
· 3 tháng trước
cảm ơn có lòng tốt nhắc nhở
miu
· 3 tháng trước
khỏi
🅿🅷á🆃
· 3 tháng trước
thế thôi nhắc làm gì
miu
· 3 tháng trước
nhắc để bt chứ sao
miu
· 3 tháng trước
2k14 à?
🅿🅷á🆃
· 3 tháng trước
oke
miu
· 3 tháng trước
?
🅿🅷á🆃
· 3 tháng trước
2k14 yes
miu
· 3 tháng trước
ừ
miu
· 3 tháng trước
nhỏ v =)))
Dưới đây là phần chứng minh các công thức lượng giác cơ bản kèm giải thích tại sao chúng đúng:
1. Công thức:sin2α+cos2α=1
Chứng minh:
-
Xét tam giác vuông có góc α, giả sử cạnh huyền là 1 (đơn vị).
-
Theo định nghĩa:
sinα=huyeˆˋnđoˆˊi,cosα=huyeˆˋnkeˆˋ -
Vì huyền = 1, nên:
sinα=đoˆˊi,cosα=keˆˋ -
Áp dụng định lý Pythagoras:
(đoˆˊi)2+(keˆˋ)2=(huyeˆˋn)2=12=1 -
Thay vào:
sin2α+cos2α=1
1+tan2α=cos2α1
Chứng minh:
-
Nhớ rằng tanα=cosαsinα.
-
Bắt đầu từ công thức 1:
sin2α+cos2α=1 -
Chia cả hai vế cho cos2α (với 0cosα=0):
1cos2αsin2α+cos2αcos2α=cos2α1 -
Suy ra:
2tan2α+1=cos2α1
31+cot2α=sin2α1
Chứng minh:
-
Nhớ rằng 4cotα=sinαcosα.
-
Bắt đầu từ công thức 1:
sin2α+cos2α=1 -
Chia cả hai vế cho 6sin2α (với 7sinα=0):
8sin2αsin2α+sin2αcos2α=sin2α1 -
Suy ra:
31+cot2α=sin2α1
0tanα⋅cotα=1
Chứng minh:
-
Thay tanα=cosαsinα, 4cotα=sinαcosα, ta có:
3tanα⋅cotα=cosαsinα⋅sinαcosα=1
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
134901
Đã trả lời bởi chuyên gia
134901 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
76057
Đã trả lời bởi chuyên gia
76057 -
 Đã trả lời bởi chuyên gia
71711
Đã trả lời bởi chuyên gia
71711 -
 Đã trả lời bởi chuyên gia
47598
Đã trả lời bởi chuyên gia
47598
Gửi báo cáo thành công!


