Cho hình chóp S.ABC. Gọi M,N,P lần lượt là trung điểm của CA,AB,BC. Gọi D là trung điểm của SM, E thuộc SP MÀ SE=2/3 SP. Tìm giao điểm của DE và (ABC); BC và (NDE)
Quảng cáo
3 câu trả lời 566
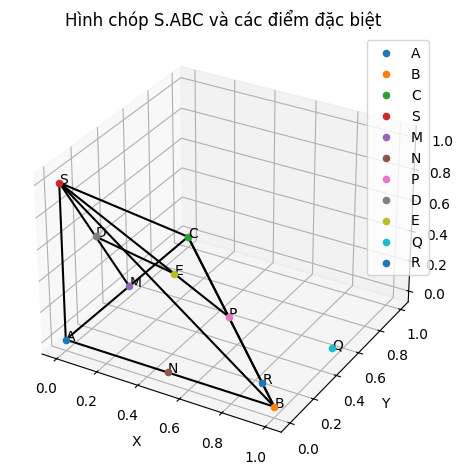 (Hình vẽ minh họa nên hơi khó nhìn chút nhé !!)
(Hình vẽ minh họa nên hơi khó nhìn chút nhé !!)

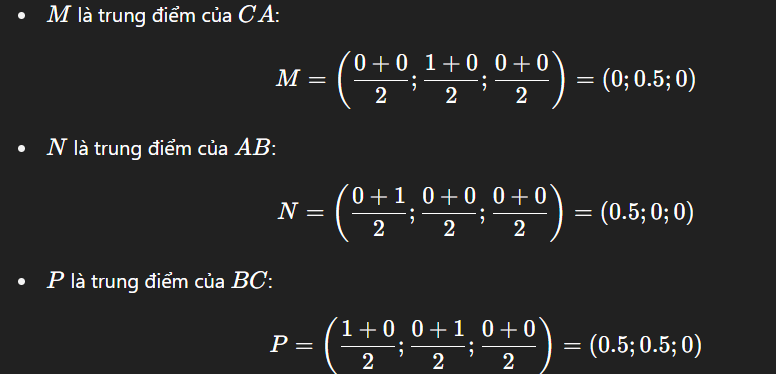
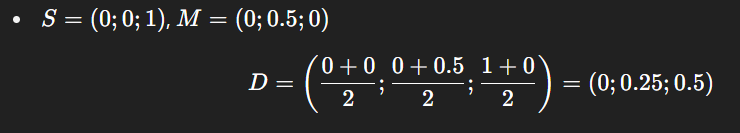
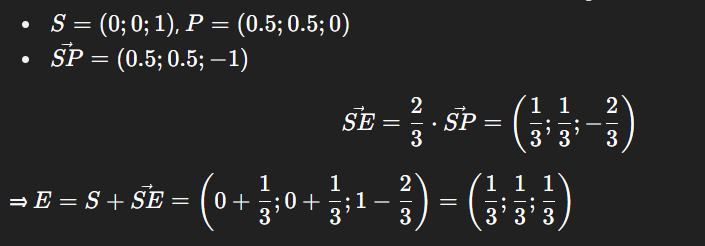


Ta cùng phân tích bài toán hình học không gian này theo từng bước cụ thể. Để dễ trình bày, ta sẽ xây dựng hệ tọa độ, tìm phương trình các mặt phẳng và các giao điểm cần thiết.
1. Tóm tắt đề bài:
Cho hình chóp S.ABCS.ABC, với:
M,N,PM, N, P lần lượt là trung điểm của các đoạn:
M∈CAM \in CA
N∈ABN \in AB
P∈BCP \in BC
DD là trung điểm của đoạn SMSM
E∈SPE \in SP, sao cho SE=23SPSE = \frac{2}{3}SP
Yêu cầu:
Tìm giao điểm của DEDE và mặt phẳng (ABC)(ABC)
Tìm giao điểm của BCBC và mặt phẳng (NDE)(NDE)
2. Gán tọa độ để giải bài toán
Giả sử:
A(0,0,0)A(0,0,0)
B(2,0,0)B(2,0,0)
C(0,2,0)C(0,2,0)
Ta chọn mặt phẳng đáy ABCABC nằm trên mặt phẳng OxyOxy, suy ra (ABC):z=0(ABC): z = 0
Chọn điểm S(0,0,h)S(0,0,h) với h>0h > 0
Tính tọa độ các điểm trung điểm:
MM là trung điểm của CACA:
M=C+A2=(0+02,2+02,0+02)=(0,1,0)M = \frac{C + A}{2} = \left( \frac{0+0}{2}, \frac{2+0}{2}, \frac{0+0}{2} \right) = (0, 1, 0)
NN là trung điểm của ABAB:
N=A+B2=(0+22,0+02,0+02)=(1,0,0)N = \frac{A + B}{2} = \left( \frac{0+2}{2}, \frac{0+0}{2}, \frac{0+0}{2} \right) = (1, 0, 0)
PP là trung điểm của BCBC:
P=B+C2=(2+02,0+22,0+02)=(1,1,0)P = \frac{B + C}{2} = \left( \frac{2+0}{2}, \frac{0+2}{2}, \frac{0+0}{2} \right) = (1, 1, 0)
3. Tính các điểm DD và EE
DD là trung điểm của đoạn SMSM:
S=(0,0,h),M=(0,1,0)⇒D=S+M2=(0,12,h2)S = (0, 0, h), \quad M = (0,1,0) \Rightarrow D = \frac{S + M}{2} = \left( 0, \frac{1}{2}, \frac{h}{2} \right)E∈SPE \in SP, với SE=23SPSE = \frac{2}{3} SP:
Tính vector SP⃗=P−S=(1,1,−h)\vec{SP} = P - S = (1,1,-h)
Vậy:
E=S+23SP⃗=(0,0,h)+23(1,1,−h)=(23,23,h−23h)=(23,23,h3)E = S + \frac{2}{3}\vec{SP} = (0,0,h) + \frac{2}{3}(1,1,-h) = \left( \frac{2}{3}, \frac{2}{3}, h - \frac{2}{3}h \right) = \left( \frac{2}{3}, \frac{2}{3}, \frac{h}{3} \right)
4. Giao điểm của đường thẳng DEDE và mặt phẳng (ABC)(ABC)
(ABC)(ABC) có phương trình: z=0z = 0
Ta tìm điểm thuộc DEDE có hoành độ z=0z = 0
Viết tham số đường thẳng DEDE:
D=(0,12,h2)D = (0, \frac{1}{2}, \frac{h}{2})
E=(23,23,h3)E = \left( \frac{2}{3}, \frac{2}{3}, \frac{h}{3} \right)
Ta có vector chỉ phương:
DE⃗=E−D=(23,16,−h6)\vec{DE} = E - D = \left( \frac{2}{3}, \frac{1}{6}, -\frac{h}{6} \right)Tham số điểm thuộc đường thẳng DEDE là:
x=23t,y=12+16t,z=h2−h6tx = \frac{2}{3}t,\quad y = \frac{1}{2} + \frac{1}{6}t,\quad z = \frac{h}{2} - \frac{h}{6}tGiải phương trình z=0⇒h2−h6t=0⇒t=3z = 0 \Rightarrow \frac{h}{2} - \frac{h}{6}t = 0 \Rightarrow t = 3
Thay vào x,yx, y:
x=23⋅3=2,y=12+16⋅3=12+12=1x = \frac{2}{3} \cdot 3 = 2, \quad y = \frac{1}{2} + \frac{1}{6} \cdot 3 = \frac{1}{2} + \frac{1}{2} = 1Vậy giao điểm là:
I=(2,1,0)I = (2, 1, 0)
5. Giao điểm của BCBC và mặt phẳng (NDE)(NDE)
Tìm mặt phẳng (NDE)(NDE)
Các điểm N(1,0,0),D(0,12,h2),E(23,23,h3)N(1,0,0), D(0, \frac{1}{2}, \frac{h}{2}), E(\frac{2}{3}, \frac{2}{3}, \frac{h}{3})
Tính 2 vector:
ND⃗=D−N=(−1,12,h2)\vec{ND} = D - N = (-1, \frac{1}{2}, \frac{h}{2}) NE⃗=E−N=(−13,23,h3)\vec{NE} = E - N = (-\frac{1}{3}, \frac{2}{3}, \frac{h}{3})Tính vector pháp tuyến n⃗=ND⃗×NE⃗\vec{n} = \vec{ND} \times \vec{NE}
Sử dụng tích có hướng:
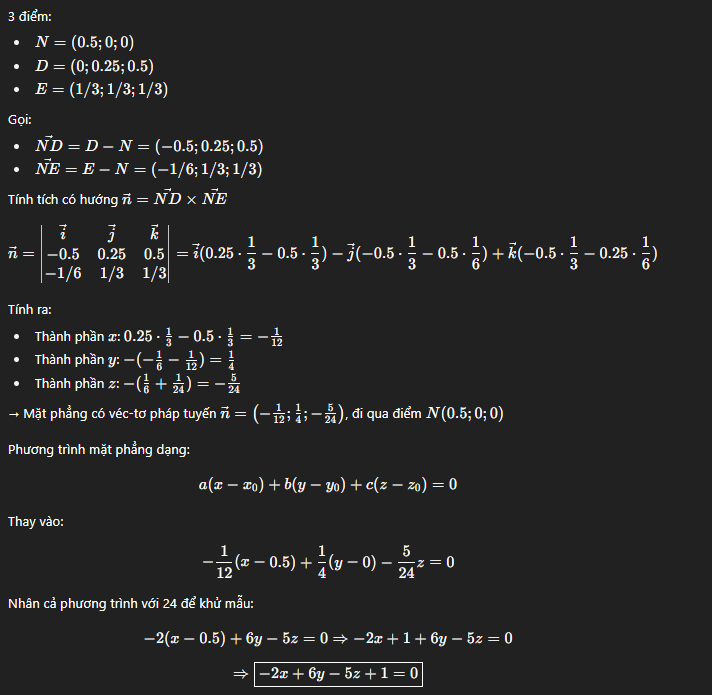
n⃗=∣ijk−112h2−1323h3∣\vec{n} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ -1 & \frac{1}{2} & \frac{h}{2} \\ -\frac{1}{3} & \frac{2}{3} & \frac{h}{3} \end{vmatrix}Tính từng thành phần:
Hoành độ: 12⋅h3−h2⋅23=h6−h3=−h6\frac{1}{2} \cdot \frac{h}{3} - \frac{h}{2} \cdot \frac{2}{3} = \frac{h}{6} - \frac{h}{3} = -\frac{h}{6}
Tung độ: −(−1⋅h3−h2⋅(−13))=−(−h3+h6)=−(−h6)=h6-\left( -1 \cdot \frac{h}{3} - \frac{h}{2} \cdot (-\frac{1}{3}) \right) = -\left( -\frac{h}{3} + \frac{h}{6} \right) = -(-\frac{h}{6}) = \frac{h}{6}
Cao độ: −1⋅23−12⋅(−13)=−23+16=−12-1 \cdot \frac{2}{3} - \frac{1}{2} \cdot (-\frac{1}{3}) = -\frac{2}{3} + \frac{1}{6} = -\frac{1}{2}
Vậy vector pháp tuyến n⃗=(−h6,h6,−12)\vec{n} = \left( -\frac{h}{6}, \frac{h}{6}, -\frac{1}{2} \right)
Phương trình mặt phẳng đi qua N(1,0,0)N(1,0,0), có vector pháp tuyến trên:
−h6(x−1)+h6(y−0)−12(z−0)=0- \frac{h}{6}(x - 1) + \frac{h}{6}(y - 0) - \frac{1}{2}(z - 0) = 0Nhân với 6 để khử mẫu:
−h(x−1)+hy−3z=0⇒−hx+h+hy−3z=0⇒−hx+hy−3z+h=0-h(x - 1) + h y - 3z = 0 \Rightarrow -h x + h + h y - 3z = 0 \Rightarrow -hx + hy - 3z + h = 0Viết tham số đoạn thẳng BCBC
B=(2,0,0),C=(0,2,0)B = (2,0,0), C = (0,2,0)
Tham số:
x=2−2t,y=2t,z=0,t∈[0,1]x = 2 - 2t,\quad y = 2t,\quad z = 0,\quad t \in [0,1]Thay vào phương trình mặt phẳng:
−hx+hy−3z+h=0⇒−h(2−2t)+h(2t)+h=0-hx + hy - 3z + h = 0 \Rightarrow -h(2 - 2t) + h(2t) + h = 0 −2h+2ht+2ht+h=0⇒4ht−h=0⇒t=14-2h + 2ht + 2ht + h = 0 \Rightarrow 4ht - h = 0 \Rightarrow t = \frac{1}{4}Thay vào x,yx, y:
x=2−x = 2 -
Quảng cáo
Bạn muốn hỏi bài tập?


