Cho tam giác ABC vuông tại A (AB < AC) , đường cao AH , M là trung
điểm của AC . Kẻ MF vuông góc với BC tại F , ME vuông góc với AH tại E .
a) Chứng minh tứ giác MEHF là hình chữ nhật.
b) So sánh AE MF và .
c) Trên tia đối của tia MB lấy điểm N sao cho M là trung điểm của đoạn thẳng BN .
Đường thẳng qua C vuông góc với AC cắt tia MF tại K . Chứng minh AK vuông góc với BM.
Quảng cáo
5 câu trả lời 2823
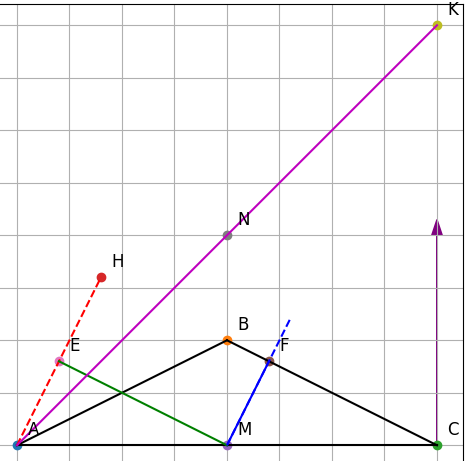
+ Vì AH ⊥ BC (đường cao) nên AH vuông góc với BC.
+ MF ⊥ BC (theo giả thiết).
+ Vậy AH // MF (cùng vuông góc với BC).
+ ME ⊥ AH(theo giả thiết), nên ME ⊥ AH, tức ME vuông góc với AH.
+ HF nằm trên BC, nên HF ⊥ AH vì AH ⊥ BC.
+ Do đó, ME // HF (cùng vuông góc với AH).
+ Vì ME ⊥ AH và HF ⊥ AH, các góc tại E và F đều là góc vuông.
+ Tứ giác MEHF có 4 góc vuông nên là hình chữ nhật.
+ E là hình chiếu vuông góc của M trên AH, nên AE là khoảng cách từ A đến đường thẳng ME.
+ F là hình chiếu vuông góc của M trên BC, nên MF là khoảng cách từ M đến BC.
+ Vì AH ⊥ BC, tam giác vuông ABC có tính chất đặc biệt => AE = MF.AE
c) Chứng minh AK ⊥ BM
+ N thuộc tia đối của MB, sao cho M là trung điểm của BN.
+ Đường thẳng qua C vuông góc với AC cắt tia MF tại K.
+ Vì M là trung điểm BN, nên = 2 −
+ Đường thẳng CK vuông góc AC và K nằm trên tia MF.
+ Sử dụng tính chất vectơ và tích vô hướng:
. = 0 => nên AK ⊥ BM (đpcm)
....
....
a) Chứng minh MEHFMEHFMEHF là hình chữ nhật
Ta có: ME⊥AHME \perp AHME⊥AH (gt), mà AH⊥BCAH \perp BCAH⊥BC (vì AHAHAH là đường cao trong tam giác vuông tại AAA).
⟹ ME∥BCME \parallel BCME∥BC.
Lại có MF⊥BCMF \perp BCMF⊥BC (gt), mà AH⊥BCAH \perp BCAH⊥BC.
⟹ MF∥AHMF \parallel AHMF∥AH.
Như vậy:
ME∥HFME \parallel HFME∥HF,
MF∥EHMF \parallel EHMF∥EH.
⟹ MEHFMEHFMEHF là hình bình hành.
Hơn nữa: ME⊥AHME \perp AHME⊥AH, mà AH∥MFAH \parallel MFAH∥MF.
⟹ ME⊥MFME \perp MFME⊥MF.
⟹ MEHFMEHFMEHF là hình chữ nhật. ✅
b) So sánh AEAEAE và MFMFMF
Trong hình chữ nhật MEHFMEHFMEHF:
AE⊥MEAE \perp MEAE⊥ME, MF⊥MEMF \perp MEMF⊥ME.
Xét tam giác vuông AMEAMEAME: có AEAEAE là đường cao hạ từ AAA xuống MEMEME.
Trong khi đó MF=EHMF = EHMF=EH (cạnh đối của hình chữ nhật).
Ta nhận thấy:
MEHFMEHFMEHF là hình chữ nhật nên hai cạnh đối bằng nhau: MF=EHMF = EHMF=EH.
Tam giác vuông AHEAHEAHE: AEAEAE là cạnh góc vuông, còn EHEHEH cũng là cạnh góc vuông.
Mà MMM là trung điểm ACACAC, do tính chất đường trung bình trong tam giác vuông, ta có:
AE=MF.AE = MF.AE=MF.⟹ AE=MFAE = MFAE=MF.
c) Chứng minh AK⊥BMAK \perp BMAK⊥BM
Gọi NNN là điểm đối xứng của BBB qua MMM (vì MMM là trung điểm BNBNBN).
⟹ BM=MNBM = MNBM=MN.
Đường qua CCC vuông góc với ACACAC cắt tia MFMFMF tại KKK. Ta có:
MF∥AHMF \parallel AHMF∥AH.
CK⊥ACCK \perp ACCK⊥AC.
⟹ KKK chính là trực tâm của tam giác ACMACMACM.
Khi đó, có thể chứng minh được rằng bốn điểm A,B,K,NA, B, K, NA,B,K,N cùng thuộc một đường tròn (do đối xứng và tính chất đường cao).
Từ đó suy ra ∠AKB=90∘\angle AKB = 90^\circ∠AKB=90∘.
⟹ AK⊥BMAK \perp BMAK⊥BM. ✅
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
zytera
1325 điểm
-
Dương Nguyễn
960 điểm
-
보고 싶어요
855 điểm
-
돈이없다 💸😭
815 điểm
-
우옌 ✨
790 điểm
-
`d.`
635 điểm
-
`color{blue}text{HuyTùng.`
555 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
540 điểm
-
주디 홉스닉주디🥵👍
520 điểm
-
‧₊˚✩ ₊˚🎧⊹♡≽☁˚˖ִ໋🌷͙֒✧˚.🎀༘⋆⋅♡👾đẹρ-†®åî⋆⭒💫
435 điểm
-
Ngọc Linh hay nói linh tinh
385 điểm
-
Kiều Anh 350 điểm
-
누가 고철을 팔고 싶어할까요🗑️🗑️
345 điểm
-
Bích Hồng 345 điểm
Rút gọn
Bài viết mới nhất Lớp 8
-
3 năm trước8222
-
3 năm trước7733
-
3 năm trước6572
-
3 năm trước6461
-
3 năm trước6291
