Question

Đã trả lời bởi chuyên gia

Answer 1

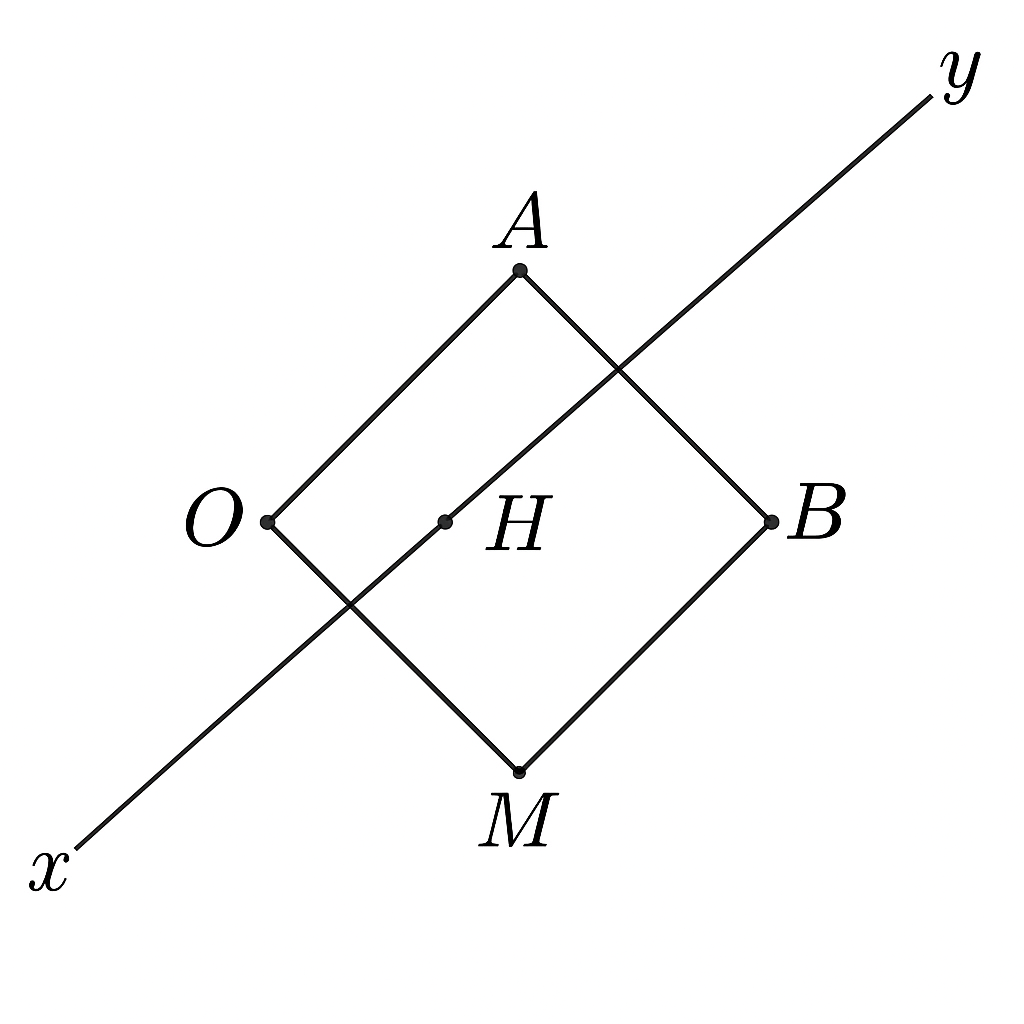Hỏi đáp VietJack + Ta xét các tam giác vuông:

Tam giác MAO có MA $⊥$ Ox, MA // Oy
Tam giác MBO có MB $⊥$ Oy, MB // Ox
Do MA // Oy, MB // Ox, và M $\in$ Ot (phân giác), nên:

MA = MB (vì đối xứng qua phân giác)
OA = OB (cùng là đoạn vuông góc từ O đến các đường thẳng song song)
⇒ Các cạnh OA = MB, OB = MA

+ Tứ giác OAMB có:

OA = MB, OB = MA
MA // Oy, OB // MA
MB // Ox, OA // MB
⇒ Tứ giác có bốn cạnh bằng nhau và hai cặp cạnh đối song song

=> OAMB là hình thoi (đpcm)

Answer 2

Để chứng minh tứ giác OAMB là hình thoi, ta cần chứng minh nó là hình bình hành và có hai cạnh kề bằng nhau (hoặc hai đường chéo vuông góc hoặc một đường chéo là phân giác góc), hoặc hai đường chéo là trung trực của nhau. Tuy nhiên, đề bài yêu cầu chứng minh OAMB là hình thoi, nhưng đề bài lại cho M thuộc Ot, MA song song Oy và MB song song Bx, với A thuộc Ox, B thuộc Oy. Các thông tin này không đủ để chứng minh OAMB là hình thoi theo định nghĩa của hình thoi, mà có thể dẫn đến hình bình hành. Có thể đề bài có sự nhầm lẫn, vì theo đề bài, ta có thể chứng minh OAMB là hình bình hành.
Cách chứng minh OAMB là hình bình hành:
Tìm góc: Vì Ot là tia phân giác của góc xOy, ta có góc xOt = góc yOt.
Sử dụng tính chất đường song song:MA song song Oy (B) => góc AMB = góc AOB (hai góc trong cùng phía tạo bởi hai đường thẳng song song cắt đường thẳng AB).
MB song song Ox (A) => góc AMB = góc AOB.
Suy ra hình bình hành: Vì hai cặp cạnh đối song song, nên tứ giác OAMB là hình bình hành.
Điều chỉnh đề bài để trở thành hình thoi:
Nếu đề bài là: Từ điểm M thuộc Ot, kẻ MA vuông góc với Ox tại A và MB vuông góc với Oy tại B. Khi đó:
Xét hai tam giác vuông OMA và OMB:Góc MOA = Góc MOB (Ot là tia phân giác).
OM chung.
Góc OMA = Góc OMB = 90 độ (theo giả thiết).
Từ đó, tam giác OMA = tam giác OMB (cạnh huyền - góc nhọn).
Suy ra OA = OB và MA = MB.
Vì OA = OB và hai cặp cạnh đối song song, OAMB là hình bình hành có hai cạnh kề bằng nhau, nên OAMB là hình thoi.
Kết luận:
Với giả thiết ban đầu, OAMB là hình bình hành chứ không phải hình thoi. Nếu sửa giả thiết là MA và MB vuông góc với Ox và Oy, thì OAMB sẽ là hình thoi.

...Xem thêm

Answer 3

Để chứng minh tứ giác OAMB là hình thoi, ta cần chứng minh nó là hình bình hành và có hai cạnh kề bằng nhau (hoặc hai đường chéo vuông góc hoặc một đường chéo là phân giác góc), hoặc hai đường chéo là trung trực của nhau. Tuy nhiên, đề bài yêu cầu chứng minh OAMB là hình thoi, nhưng đề bài lại cho M thuộc Ot, MA song song Oy và MB song song Bx, với A thuộc Ox, B thuộc Oy. Các thông tin này không đủ để chứng minh OAMB là hình thoi theo định nghĩa của hình thoi, mà có thể dẫn đến hình bình hành. Có thể đề bài có sự nhầm lẫn, vì theo đề bài, ta có thể chứng minh OAMB là hình bình hành.
Cách chứng minh OAMB là hình bình hành:
Tìm góc: Vì Ot là tia phân giác của góc xOy, ta có góc xOt = góc yOt.
Sử dụng tính chất đường song song:MA song song Oy (B) => góc AMB = góc AOB (hai góc trong cùng phía tạo bởi hai đường thẳng song song cắt đường thẳng AB).
MB song song Ox (A) => góc AMB = góc AOB.
Suy ra hình bình hành: Vì hai cặp cạnh đối song song, nên tứ giác OAMB là hình bình hành.
Điều chỉnh đề bài để trở thành hình thoi:
Nếu đề bài là: Từ điểm M thuộc Ot, kẻ MA vuông góc với Ox tại A và MB vuông góc với Oy tại B. Khi đó:
Xét hai tam giác vuông OMA và OMB:Góc MOA = Góc MOB (Ot là tia phân giác).
OM chung.
Góc OMA = Góc OMB = 90 độ (theo giả thiết).
Từ đó, tam giác OMA = tam giác OMB (cạnh huyền - góc nhọn).
Suy ra OA = OB và MA = MB.
Vì OA = OB và hai cặp cạnh đối song song, OAMB là hình bình hành có hai cạnh kề bằng nhau, nên OAMB là hình thoi.
Kết luận:
Với giả thiết ban đầu, OAMB là hình bình hành chứ không phải hình thoi. Nếu sửa giả thiết là MA và MB vuông góc với Ox và Oy, thì OAMB sẽ là hình thoi.

Answer 4

.. Ta có đề bài:

Cho góc xOy và tia phân giác Ot. Từ điểm M thuộc Ot, kẻ:

MA // Oy (→ A thuộc Ox)

MB // Ox (→ B thuộc Oy).
Chứng minh tứ giác OAMB là hình thoi.

✅ Phân tích hình học:

Ot là phân giác của góc xOy ⇒ Ot chia góc xOy thành 2 phần bằng nhau.
M ∈ Ot ⇒ M cách đều hai cạnh Ox và Oy của góc xOy.
MA // Oy ⇒ MA ⊥ Ox (vì Oy ⊥ Ox).
MB // Ox ⇒ MB ⊥ Oy.
Từ đó, xác định được:
- A ∈ Ox, MA ⊥ Ox
- B ∈ Oy, MB ⊥ Oy

⇒ Các đoạn OM, OA, OB, AM, MB có quan hệ đặc biệt về độ dài và góc.

✍️ Chứng minh: 1. Tam giác MOA vuông tại A:

Vì MA // Oy ⇒ MA ⊥ Ox (vì Ox ⊥ Oy)
⇒ MA ⊥ OA ⇒ tam giác MOA vuông tại A.

Tương tự:

MB // Ox ⇒ MB ⊥ Oy ⇒ MB ⊥ OB ⇒ tam giác MOB vuông tại B.

2. MA = MB

Vì:

MA là khoảng cách từ M đến Ox
MB là khoảng cách từ M đến Oy
M nằm trên Ot là phân giác của góc xOy
⇒ Theo tính chất tia phân giác, điểm M cách đều hai cạnh của góc xOy
⇒ MA = MB

3. OA = OB

MA ⊥ OA và MB ⊥ OB
MA = MB
∠OMA = ∠OMB (vì Ot là phân giác)
⇒ Tam giác MOA và MOB bằng nhau (góc – cạnh – góc)

⇒ OA = OB

4. Kết luận:

Tứ giác OAMB có:

MA = MB (2 cạnh kề bằng nhau)
OA = OB (2 cạnh còn lại bằng nhau)
MA ⊥ OA và MB ⊥ OB ⇒ các cạnh liên tiếp vuông góc với nhau

⇒ Tứ giác có 4 cạnh bằng nhau và hai cặp cạnh liên tiếp vuông góc
⇒ OAMB là hình thoi

✅ Kết luận cuối cùng:

Tứ giác OAMB là hình thoi.

(Nếu cần hình vẽ hoặc chứng minh bằng tọa độ, mình có thể cung cấp thêm.)