Quảng cáo
5 câu trả lời 281
+ Sử dụng tính chất góc kề bù:
Hai góc kề bù có tổng bằng 180∘: + =180∘ ⇒ =180∘ − 80∘ = 100∘
+ Vì Om là phân giác của = 80∘, nên: = .80∘ = 40∘
+ Vì On là phân giác của = 100∘, nên: = .100∘ = 50∘
+ Do và nằm về hai phía của tia Oy, nên:
1 = + = 40∘ + 50∘ = 90∘
✅ KẾT QUẢ CUỐI CÙNG:
mOy = 40°
nOy = 50°
mOn = 90°
∠mOy=40∘
∠nOy=50∘
Các góc cần tìm là:
mOy=40∘
nOy=50∘
mOn=90∘
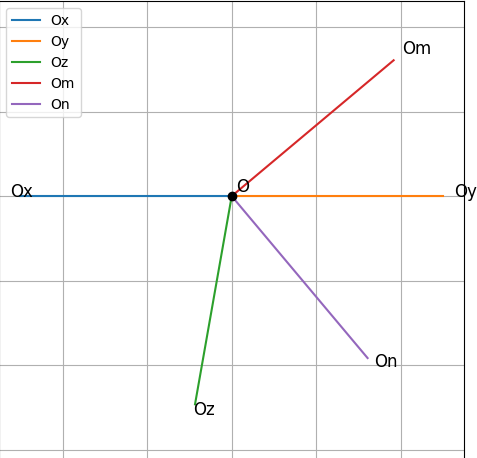
### Cách vẽ hình
1. **Vẽ góc xOy:**
* Vẽ tia Ox.
* Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ tia Oy sao cho góc $xOy = 80^\circ$.
2. **Vẽ góc yOz:**
* Vẽ tia Oz là tia đối của tia Ox. Khi đó, góc xOy và yOz là hai góc kề bù.
3. **Vẽ tia phân giác Om:**
* Vẽ tia Om nằm giữa hai tia Ox và Oy sao cho góc $xOm = mOy = \frac{1}{2}xOy = \frac{1}{2} \times 80^\circ = 40^\circ$.
4. **Vẽ tia phân giác On:**
* Vẽ tia On nằm giữa hai tia Oy và Oz.
***
### Tính toán các góc
Ta có:
* **Tính $mOy$:**
* Vì Om là tia phân giác của góc xOy nên $mOy = \frac{1}{2} \times xOy = \frac{1}{2} \times 80^\circ = 40^\circ$.
* **Tính $nOy$:**
* Vì xOy và yOz là hai góc kề bù, nên tổng số đo của chúng là $180^\circ$.
* $xOy + yOz = 180^\circ \implies 80^\circ + yOz = 180^\circ \implies yOz = 180^\circ - 80^\circ = 100^\circ$.
* Vì On là tia phân giác của góc yOz nên $nOy = \frac{1}{2} \times yOz = \frac{1}{2} \times 100^\circ = 50^\circ$.
* **Tính $mOn$:**
* Vì tia Oy nằm giữa hai tia Om và On, nên $mOn = mOy + nOy$.
* $mOn = 40^\circ + 50^\circ = 90^\circ$.
Vậy, các góc cần tìm là:
* $mOy = 40^\circ$
* $nOy = 50^\circ$
* $mOn = 90^\circ$
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120761
-
81498
-
59515
-
zytera
1325 điểm
-
Dương Nguyễn
960 điểm
-
보고 싶어요
855 điểm
-
돈이없다 💸😭
815 điểm
-
우옌 ✨
790 điểm
-
`d.`
635 điểm
-
`color{blue}text{HuyTùng.`
555 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
540 điểm
-
주디 홉스닉주디🥵👍
520 điểm
-
‧₊˚✩ ₊˚🎧⊹♡≽☁˚˖ִ໋🌷͙֒✧˚.🎀༘⋆⋅♡👾đẹρ-†®åî⋆⭒💫
435 điểm
-
Ngọc Linh hay nói linh tinh
385 điểm
-
Kiều Anh 350 điểm
-
누가 고철을 팔고 싶어할까요🗑️🗑️
345 điểm
-
Bích Hồng 345 điểm
Rút gọn
Bài viết mới nhất Lớp 7
-
2 năm trước4934
