Cho hình chóp S.ABCD với ABCD là hình bình hành. Gọi M là điểm bất kỳ thuộc SB,

Minh Lê Hỏi từ APP VIETJACK

· 16:05 19/08/2025

Cho hình chóp S.ABCD với ABCD là hình bình hành. Gọi M là điểm bất kỳ thuộc SB, N thuộc miền trong tam giác SCD.

1. Tìm giao điểm của MN và mặt phẳng (ABCD).

2. Tim SCO (AMN), SD∩ (AMN).

3. Tim SAN (CMN).

Trả Lời (+5 điểm)

Hỏi chi tiết

Quảng cáo

3 câu trả lời 3556

Gia Hân

4 tháng trước

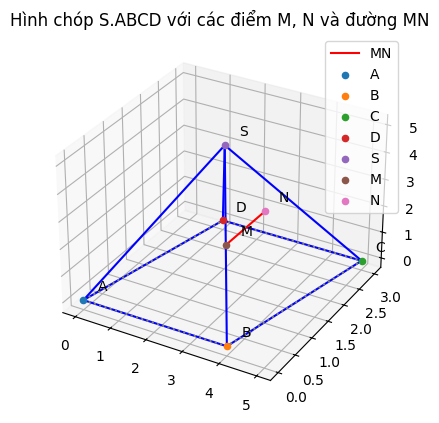
Hỏi đáp VietJack

1,Tìm giao điểm của MN và mặt phẳng (ABCD)

Xét mặt phẳng (SCD):
N ∈ △SCD ⇒ N ∈ (SCD)
MN ⊂ (MSN) , mặt phẳng chứa hai điểm M,N
Mặt phẳng (MSN) cắt mặt phẳng đáy (ABCD) theo giao tuyến
⇒ Giao điểm của MN với mặt đáy (ABCD) chính là giao điểm của đường thẳng MN với mặt phẳng (ABCD)

➡ Gọi P = MN ∩ (ABCD)\

=> P là điểm giao của MN với mặt phẳng đáy

2. Tìm SC ∩ (AMN), và SD ∩ (AMN)

Gọi I = SC ∩ (AMN)
Vì C ∈ (ABCD), S là đỉnh chóp, nên SC là cạnh bên
+ Xét 2 mặt phẳng giao nhau tại điểm
Trong (AMN), dựng 2 đường thẳng cắt nhau:

AM
AN
Dựng mặt phẳng (AMN), cắt đường thẳng SC
⇒ Lấy 2 mặt phẳng (SCN) và (AMN), cắt nhau theo giao tuyến

→ Giao điểm của SC với (AMN) là điểm thuộc SC và đồng thời thuộc (AMN)

=> I là điểm chung của SC và mặt phẳng (AMN)

Tương tự:

Tìm SD ∩ (AMN)
Gọi J = SD ∩ (AMN)

⇒ Dùng phương pháp tương tự để xác định điểm cắt

3. Tìm giao tuyến của (SAN) và (CMN)

Hai mặt phẳng (SAN) và (CMN) có điểm chung là N (vì N thuộc cả hai tam giác)
Dựng hai đường thẳng trong mỗi mặt phẳng:

Trong (SAN): lấy SA,AN
Trong (CMN): lấy CM, MN
⇒ Dựng hai mặt phẳng, tìm giao tuyến chung đi qua N

Giao tuyến là đường thẳng qua điểm N, đồng thời nằm trong cả hai mặt phẳng (SAN) và (CMN) → là giao tuyến của hai mặt phẳng này

...Xem thêm

0 bình luận

Đăng nhập để hỏi chi tiết

♉︎𓍢🎧ＡＮ_Ｍê_ＯＴＰ_Dương _Ｈùng ✧˚.🎀༘⋆✧

4 tháng trước

1. Xác định mặt phẳng phụ chứa MN:
Chọn mặt phẳng (SBD) chứa đường thẳng MN (vì M thuộc SB).
2. Tìm giao tuyến của mặt phẳng phụ và mặt phẳng (ABCD):
Giao tuyến của (SBD) và (ABCD) là đường thẳng BD.
3. Tìm giao điểm của MN với giao tuyến:
Gọi I là giao điểm của MN và BD.
4. Kết luận:
I chính là giao điểm của MN và mặt phẳng (ABCD).
Bài 2: Tìm giao tuyến của mặt phẳng (AMN) với các mặt phẳng (SCD) và (SBC)
Tìm giao tuyến của (AMN) và (SCD):
1. N thuộc cả (AMN) và (SCD).

2. Kéo dài AN cắt CD tại P. P thuộc (AMN) và (SCD).

3. Giao tuyến là đường thẳng NP.

Tìm giao tuyến của (AMN) và (SBC):
1. M thuộc cả (AMN) và (SBC).

2. Kéo dài AM cắt BC tại Q. Q thuộc (AMN) và (SBC).

3. Giao tuyến là đường thẳng MQ.

Bài 3: Tìm giao tuyến của mặt phẳng (CMN) với mặt phẳng (SAN)
1. N thuộc cả (CMN) và (SAN).

2. Xác định một điểm chung khác:
Kéo dài CM cắt AB tại R. R thuộc (CMN).
Kéo dài SN cắt AD tại T. T thuộc (SAN).
Tìm giao điểm của RN và AT. (Đây là một cách phức tạp hơn).
Cách khác: Tìm giao điểm của CN với mặt phẳng (SAB), hoặc CM với (SAD).
Nếu N nằm trên cạnh SD, thì giao tuyến là SN.
Nếu N là điểm bất kỳ trong tam giác SCD, ta cần tìm một điểm chung khác.
Gọi K là giao điểm của CN và SD.
Gọi L là giao điểm của MN và (SAD).
Giao tuyến của (CMN) và (SAN) sẽ đi qua N và một điểm khác.
Tìm giao điểm của CM với mặt phẳng (SAD). Kéo dài CM cắt AD tại X, thì X thuộc (CMN) và (SAD).
Tuy nhiên, X không chắc thuộc (SAN).
Tìm giao điểm của AN và CM. Nếu chúng cắt nhau, đó là một điểm chung.
Nếu không, ta cần tìm một điểm chung khác bằng cách tìm giao điểm của một đường thẳng trong (CMN) với một đường thẳng trong (SAN).
Ví dụ: Tìm giao điểm của CM và (SAD). Kéo dài CM cắt AD tại I. I thuộc (CMN). I cũng thuộc (SAD). Nếu I nằm trên AN, thì N và I là hai điểm chung.
Nếu không, ta cần tìm giao điểm của một đường thẳng khác.
Xét mặt phẳng (SCD) chứa N. Giao tuyến của (CMN) và (SAD) là đường thẳng đi qua N và giao điểm của CM và SD (nếu có).
Giao tuyến của (CMN) và (SAN) là đường thẳng đi qua N và giao điểm của CM với mặt phẳng (SAN) (nếu có).
Để đơn giản hóa bài 3:
Tìm giao tuyến của (CMN) và (SAD).
Tìm giao tuyến của (SAN) và (SCD).
Giao tuyến của (CMN) và (SAN) sẽ đi qua N và giao điểm của đường thẳng CM với mặt phẳng (SAN) (nếu có).
Hoặc tìm giao điểm của AN với CM, nếu có.
Một cách tiếp cận khác: Tìm giao điểm của CM với mặt phẳng (SAD). Gọi E là giao điểm của CM và SD. E thuộc (CMN) và (SAD).
Nếu E cũng thuộc AN, thì giao tuyến là AN.
Nếu không, ta cần tìm điểm chung thứ hai.
Giao tuyến là đường thẳng đi qua N và giao điểm của CM với AN.

...Xem thêm

32 bình luận

1 ( 5.0 )

hehe · 4 tháng trước

mất cau kia mất r

...Xem tất cả bình luận

Đăng nhập để hỏi chi tiết

CEO tập đoàn Tống thị

4 tháng trước

1. MN ∩ (ABCD) = I — điểm cắt đường thẳng MN với đáy, không xác định rõ, nhưng tồn tại duy nhất.
2. SC ∩ (AMN) = Q — điểm thuộc SC và SD lần lượt, giao với mặt phẳng (AMN).
3. SAN ∩ CMNSAN là đường thẳng đi qua N, gọi là d, là giao tuyến của 2 mặt phẳng.

0 bình luận

1 ( 5.0 )

Đăng nhập để hỏi chi tiết

Quảng cáo

Bạn muốn hỏi bài tập?