Bài 5: Cho tam giác cân ABC (AB = AC ). Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB, AC lần lượt ở M, N. Chứng minh rằng:
a) DM = EN
b) Đường thẳng BC cắt MN tại trung điểm I của MN.
c) Đường thẳng vuông góc với MN tại I luôn đi qua một điểm cố định khi D thay đổi trên cạnh BC
♉︎𓍢🎧ＡＮ_Ｍê_ＯＴＰ_Dương _Ｈùng ✧˚.🎀༘⋆✧
· 4 tháng trước
bạn cũng fan Lyhan hả
Quảng cáo
3 câu trả lời 293
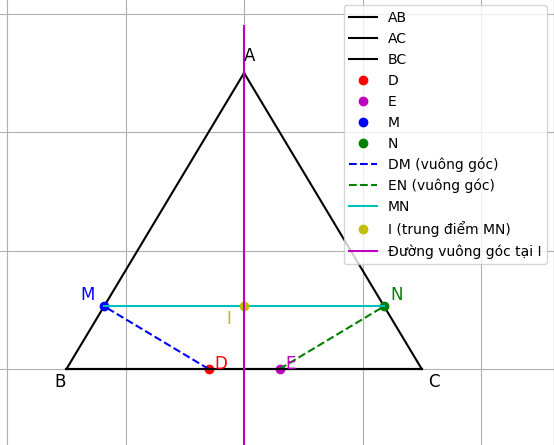
a) Chứng minh: DM = EN
Vì AB = AC, tam giác cân nên góc tại A cân đối.
Đường vuông góc từ D đến AB và từ E đến AC tạo thành hai tam giác vuông có cạnh huyền là
Đường vuông góc từ D đến AB và từ E đến AC tạo thành hai tam giác vuông có cạnh huyền là
AB = AC .
Do BD = CE và D, E nằm trên cùng một đường thẳng BC (với E ở phía ngoài), khoảng cách từ D đến B bằng khoảng cách từ C đến E.
Hai tam giác vuông DMB và ENC đồng dạng và bằng nhau theo cạnh huyền và góc nhọn kề cạnh.
=> DM = EN.
Do BD = CE và D, E nằm trên cùng một đường thẳng BC (với E ở phía ngoài), khoảng cách từ D đến B bằng khoảng cách từ C đến E.
Hai tam giác vuông DMB và ENC đồng dạng và bằng nhau theo cạnh huyền và góc nhọn kề cạnh.
=> DM = EN.
b) Chứng minh: BC cắt MN tại trung điểm I của MN.
Do tam giác cân, đường cao AI cũng là trung tuyến.
I là trung điểm của BC.
Do tính đối xứng và các đoạn vuông góc, I cũng là trung điểm của MN.
I là trung điểm của BC.
Do tính đối xứng và các đoạn vuông góc, I cũng là trung điểm của MN.
Sử dụng tính chất hình học đối xứng của tam giác cân
=> I là trung điểm của MN.
c) Chứng minh: Đường thẳng vuông góc với MN tại I luôn đi qua một điểm cố định khi D thay đổi trên cạnh BC.
Gọi P là giao điểm của đường thẳng vuông góc với MN tại I và đường thẳng AI (đường cao/đường trung tuyến).
Vì tính chất đối xứng và vuông góc của tam giác cân, P là điểm cố định.
Vì tính chất đối xứng và vuông góc của tam giác cân, P là điểm cố định.
4 tháng trước
a) Chứng minh DM=EN
Tứ giác DMEN có DM⊥BC, EN⊥BC
Tứ giác DMEN có DM⊥BC, EN⊥BC
⇒ DM // EN
Lại có BD=CE và △ABD=△ACE (cạnh – góc – cạnh vì AB=AC, A chung, BD=CE).
Suy ra △BDM=△CEN(góc vuông, cạnh huyền, cạnh góc vuông).
Do đó DM=EN. ✅
Lại có BD=CE và △ABD=△ACE (cạnh – góc – cạnh vì AB=AC, A chung, BD=CE).
Suy ra △BDM=△CEN(góc vuông, cạnh huyền, cạnh góc vuông).
Do đó DM=EN. ✅
b) Chứng minh BC cắt MN tại trung điểm của I của MN
Gọi I=BC ∩ MN
Trong △BDM và △CEN đã có DM=EN ( câu a )
Lại có BD=CE
Suy ra IM=IN
Vậy I là trung điểm của MN. ✅
Gọi I=BC ∩ MN
Trong △BDM và △CEN đã có DM=EN ( câu a )
Lại có BD=CE
Suy ra IM=IN
Vậy I là trung điểm của MN. ✅
c) Đường vuông góc với MN tại I luôn đi qua một điểm cố định
Vì I là trung điểm của MN, mà I∈BC, nên đường thẳng vuông góc với MN tại I chính là đường trung trực của MN.
Từ a) và b) ta có: khi D di chuyển trên BC, thì trung trực của MN luôn đi qua điểm A (đỉnh tam giác cân).
Do đó, tính đối xứng của tam giác cân ABC theo đường cao AH (H là trung điểm BC), nên A luôn nằm trên đường thẳng đó.
👉 Vậy, đường vuông góc với MN tại I luôn đi qua điểm cố định A. ✅
Vì I là trung điểm của MN, mà I∈BC, nên đường thẳng vuông góc với MN tại I chính là đường trung trực của MN.
Từ a) và b) ta có: khi D di chuyển trên BC, thì trung trực của MN luôn đi qua điểm A (đỉnh tam giác cân).
Do đó, tính đối xứng của tam giác cân ABC theo đường cao AH (H là trung điểm BC), nên A luôn nằm trên đường thẳng đó.
👉 Vậy, đường vuông góc với MN tại I luôn đi qua điểm cố định A. ✅
4 tháng trước
Vậy AI vuông góc với MN.
Do đó, đường thẳng vuông góc với MN tại I chính là đường thẳng AI.
Vì A là đỉnh của tam giác cân ABC và I là trung điểm của MN (MN song song với BC), nên AI luôn đi qua A.
Vậy đường thẳng vuông góc với MN tại I luôn đi qua điểm A cố định.
Do đó, đường thẳng vuông góc với MN tại I chính là đường thẳng AI.
Vì A là đỉnh của tam giác cân ABC và I là trung điểm của MN (MN song song với BC), nên AI luôn đi qua A.
Vậy đường thẳng vuông góc với MN tại I luôn đi qua điểm A cố định.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120578
-
81263
-
59365
Thành viên hăng hái nhất trong tuần
-
돈이없다 💸😭
435 điểm
-
반짝이는 달 420 điểm
-
야연 ✨
400 điểm
-
보고 싶어요
385 điểm
-
jet jet #
345 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
305 điểm
-
`d.`
285 điểm
-
Kiều Anh 170 điểm
-
Phát: ''đạp = niềm tin hả?''; t : ''🤫🧏''
135 điểm
-
`color{blue}text{이 글을 읽는 사람은 바보다.`베트남이 챔피언입니다.
105 điểm
-
Hung Hungdoan 100 điểm
-
baolam<3
70 điểm
-
Paris.khong.co.em...
70 điểm
-
Judy Hopps
60 điểm
Rút gọn
Bài viết mới nhất Lớp 7
-
2 năm trước4926
Gửi báo cáo thành công!
