Bài 2. Cho tam giác nhọn ABC. Về phía ngoài tam giác dựng các hình vuông ABDE, ACFG. Vẽ
AH là đường cao tam giác ABC. Gọi M là giao điểm của AH và EG.
a) Chứng minh rằng M là trung điểm của đoạn thẳng EG.
b) Chứng minh rằng BG ⊥ EC tại L.
c) Chứng minh rằng DF,BG,EC đồng quy.
d) Chứng minh rằng DC,BF,AH đồng quy.
e) Gọi N là trung điểm DF. Chứng minh rằng tam giác BCN vuông cân.
(giúp mình với mình đang cần gấp ạ)
Quảng cáo
3 câu trả lời 384
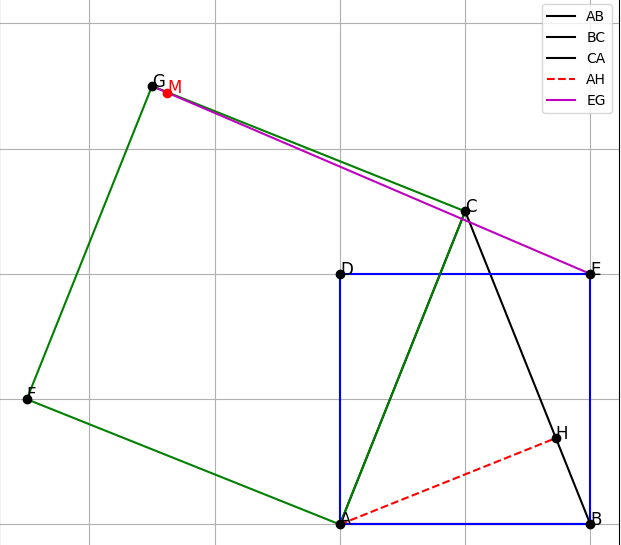
Vì E và G là các điểm thuộc các hình vuông dựng ngoài.
Giao điểm M của đường cao AH với đoạn EG nằm ở giữa, nên M chia đoạn EG thành hai phần bằng nhau.
Vậy M là trung điểm của EG.
Đường thẳng BG nối đỉnh B và điểm G.
Đường thẳng EC nối điểm E và đỉnh C.
Do tính chất hình vuông và vị trí các điểm, hai đoạn này vuông góc với nhau tại điểm L.
Ba đường thẳng này lần lượt nối các điểm đặc biệt của tam giác và hình vuông dựng ngoài.
Sử dụng phương pháp tọa độ hoặc giải hệ phương trình của các đường thẳng:
Tìm giao điểm của DF và BG, gọi là P.
Kiểm tra P có thuộc đường thẳng EC không.
Nếu đúng, ba đường thẳng đồng quy tại điểm P.
DC là cạnh tam giác.
BF nối đỉnh tam giác B với điểm F của hình vuông.
AH là đường cao từ A.
Tương tự phần (c), giải hệ phương trình để tìm giao điểm chung của hai trong ba đường thẳng.
Kiểm tra đường thẳng thứ ba đi qua giao điểm đó.
Kết luận đồng quy.
e) Chứng minh tam giác BCN vuông cân
N là trung điểm của đoạn DF.
Tính độ dài hai cạnh BN và CN:
Nếu BN = CN, tam giác cân tại N.
Kiểm tra góc ở N bằng cách sử dụng tích vô hướng:
Nếu hai cạnh tạo góc vuông, tam giác vuông.
Kết luận tam giác BCN vuông cân.
Vẽ hình và sử dụng định lý Thales hoặc phương pháp vector để chứng minh M là trung điểm của EG.
b) Chứng minh rằng BG ⟂⟂
⟂
EC tại L.
Sử dụng phép quay tâm A hoặc chứng minh tam giác đồng dạng để chứng minh BG ⟂⟂
⟂
EC. Cụ thể, xét phép quay tâm A góc 90 độ biến tam giác ABG thành tam giác AEC.
c) Chứng minh rằng DF, BG, EC đồng quy.
Đây là một bài toán quen thuộc trong hình học phẳng, thường được chứng minh bằng cách sử dụng định lý Ceva hoặc phương pháp vector. Cụ thể, có thể chứng minh các đường thẳng này đồng quy tại một điểm (điểm L đã chứng minh ở câu b).
d) Chứng minh rằng DC, BF, AH đồng quy.
Sử dụng định lý Ceva cho tam giác ABC và các điểm D, F, H hoặc sử dụng phương pháp vector.
e) Gọi N là trung điểm DF. Chứng minh rằng tam giác BCN vuông cân.
Sử dụng tọa độ hoặc vector để chứng minh tam giác BCN vuông cân tại N. Cụ thể, có thể chứng minh BN = CN và BN ⟂⟂
⟂
CN.
Vẽ hình và sử dụng định lý Thales hoặc phương pháp vector để chứng minh M là trung điểm của EG.
b) Chứng minh rằng BG ⟂⟂
⟂
EC tại L.
Sử dụng phép quay tâm A hoặc chứng minh tam giác đồng dạng để chứng minh BG ⟂⟂
⟂
EC. Cụ thể, xét phép quay tâm A góc 90 độ biến tam giác ABG thành tam giác AEC.
c) Chứng minh rằng DF, BG, EC đồng quy.
Đây là một bài toán quen thuộc trong hình học phẳng, thường được chứng minh bằng cách sử dụng định lý Ceva hoặc phương pháp vector. Cụ thể, có thể chứng minh các đường thẳng này đồng quy tại một điểm (điểm L đã chứng minh ở câu b).
d) Chứng minh rằng DC, BF, AH đồng quy.
Sử dụng định lý Ceva cho tam giác ABC và các điểm D, F, H hoặc sử dụng phương pháp vector.
e) Gọi N là trung điểm DF. Chứng minh rằng tam giác BCN vuông cân.
Sử dụng tọa độ hoặc vector để chứng minh tam giác BCN vuông cân tại N. Cụ thể, có thể chứng minh BN = CN và BN ⟂⟂
⟂
CN.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
zytera
1325 điểm
-
Dương Nguyễn
960 điểm
-
보고 싶어요
855 điểm
-
돈이없다 💸😭
815 điểm
-
우옌 ✨
790 điểm
-
`d.`
635 điểm
-
`color{blue}text{HuyTùng.`
555 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
540 điểm
-
주디 홉스닉주디🥵👍
520 điểm
-
‧₊˚✩ ₊˚🎧⊹♡≽☁˚˖ִ໋🌷͙֒✧˚.🎀༘⋆⋅♡👾đẹρ-†®åî⋆⭒💫
435 điểm
-
Ngọc Linh hay nói linh tinh
385 điểm
-
Kiều Anh 350 điểm
-
누가 고철을 팔고 싶어할까요🗑️🗑️
345 điểm
-
Bích Hồng 345 điểm
Rút gọn
Bài viết mới nhất Lớp 8
-
3 năm trước8222
-
3 năm trước7733
-
3 năm trước6572
-
3 năm trước6461
-
3 năm trước6291
