Cho chóp S. ABCD có đáy là hình bình hành. Gọi M, N là trung điểm SB, SD ; P thuộc SC : PC< PS . Tìm giao tuyến của:
a) ( SAC) và (SBD)
b) ( MNP) và ( SBD)
c) ( MNP) và ( SAC).
d) (MNP) và (SAB)
e) ( MNP) và ( SAD)
f) ( MNP) và ( ABCD)
Quảng cáo
4 câu trả lời 551
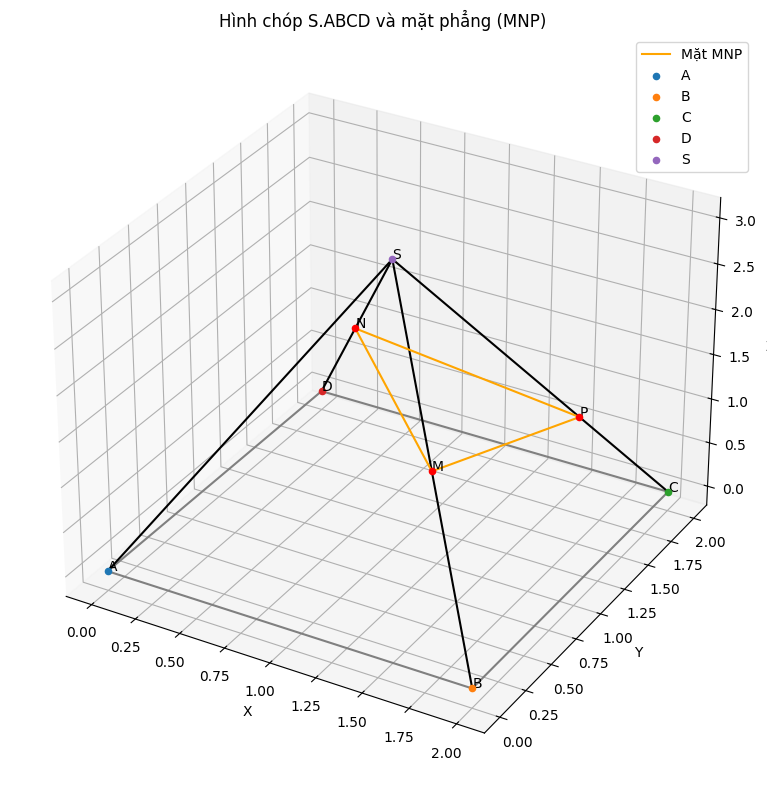
a) Giao tuyến của (SAC) và (SBD)
Ta có : S ∈ (SAC) ∩ (SBD).
Xét đường AC (thuộc đáy)
Xét đường BD (cũng thuộc đáy)
Vì ABCD là hình bình hành, hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi.
=> O ∈ AC ∩ BD, nên:
O ∈ (SAC) vì O ∈ AC.
O ∈ (SBD) vì O ∈ B.
=> Giao tuyến của (SAC) và (SBD) là đường thẳng SO, với O là giao điểm hai đường chéo AC và BD.
b) Giao tuyến của (MNP) và (SBD)
Ta có:
M ∈ SB ⇒ M ∈ (SBD).
N ∈ SD ⇒ N ∈ (SBD).
=> M, N ∈ (MNP) ∩ (SBD)
=> Giao tuyến của (MNP) và (SBD) là đường thẳng MN.
c) Giao tuyến của (MNP) và (SAC)
+ Ta có:
P ∈ SC ⇒P ∈ (SAC)
P ∈ (MNP)
+ Ta xét giao điểm của đường MN với mặt (SAC).
Gọi I = MN ∩ (SAC)(nếu có), thì:
Giao tuyến là đường thẳng đi qua P và I.
=> Giao tuyến của (MNP) và (SAC) là đường thẳng đi qua P và giao điểm I của MN với mặt phẳng (SAC).
d) Giao tuyến của (MNP) và (SAB)
Ta có: Mặt phẳng (SAB): chứa S, A, B
+ Vì M ∈ SB, S,B ∈ (SAB), nên M ∈ (SAB)
P ∈ SC, C ∉ (SAB)
Vậy đường thẳng MP cắt mặt phẳng (SAB) tại đúng 1 điểm: M
=> Giao tuyến của (MNP) và (SAB) là đường thẳng đi qua điểm M và giao điểm của mặt phẳng (SAB) với mặt phẳng (MNP) → chính là giao điểm của (SAB) với mặt MNP tại đường thẳng qua M và điểm I (giao điểm của đoạn NP với (SAB))
=> Giao tuyến là đường thẳng qua M và giao điểm I ∈ NP ∩ (SAB)
e) Giao tuyến của (MNP) và (SAD)
Tương tự câu d.
N ∈ SD ⇒ N ∈ (SAD)
M ∈ SB, P ∈ SC, không thuộc (SAD)
=> Có 1 điểm chung là N
Giao tuyến đi qua N, cần thêm 1 điểm nữa → tìm giao điểm Q = MP ∩ (SAD)
=> Giao tuyến là đường thẳng đi qua N và giao điểm của đường MP với mặt phẳng (SAD)
f) Giao tuyến của (MNP) và (ABCD)
Mặt ABCD là đáy hình chóp
MNP nằm hoàn toàn trên các cạnh bên (không có điểm nào chắc chắn thuộc đáy)
→ Không có điểm chung rõ ràng
Tuy nhiên, nếu đường thẳng NP cắt mặt đáy tại 1 điểm → giao tuyến là 1 đoạn thẳng.
=> Giao tuyến là đường thẳng qua điểm Q = NP ∩ (ABCD) nếu có.
Nếu không, (MNP) và (ABCD) không cắt nhau hoặc giao tuyến là rỗng.
(Từ hình minh họa trên bạn kẻ thêm đường và các giao điểm để dễ nhìn hơn nhé )
a) Giao tuyến của (SAC) và (SBD) là SO, với O là giao điểm của AC và BD. Vì ABCD là hình bình hành nên AC và BD cắt nhau tại trung điểm của mỗi đường. Gọi O là giao điểm của AC và BD, thì O thuộc AC (do O thuộc AC) và O thuộc BD (do O thuộc BD). Vậy O thuộc (SAC) và O thuộc (SBD). Mặt khác, S cũng thuộc (SAC) và (SBD). Do đó, giao tuyến của (SAC) và (SBD) là đường thẳng đi qua S và O, chính là SO.
b) Giao tuyến của (MNP) và (SBD) là NP. Vì M và N là trung điểm của SB và SD, nên MN // BD (đường trung bình trong tam giác SBD). Mặt khác, BD nằm trong (SBD). Do đó, MN // (SBD). Vì P thuộc SC, nên giao tuyến của (MNP) và (SBD) là đường thẳng đi qua N và song song với BD. Vì MN // BD, và N thuộc SD, nên đường thẳng cần tìm chính là đường thẳng NP. Vậy giao tuyến của (MNP) và (SBD) là NP.
c) Giao tuyến của (MNP) và (SAC) là PX, với X là giao điểm của AC và NP. Vì P thuộc SC và N là trung điểm của SD, nên NP không song song với SC. Do đó, NP và SC cắt nhau tại một điểm, gọi là X. Vì X thuộc NP, và NP thuộc (MNP), nên X thuộc (MNP). Vì X thuộc SC, nên X thuộc (SAC). Vậy, giao tuyến của (MNP) và (SAC) là đường thẳng đi qua P và X. Vì X là giao điểm của NP và AC, nên giao tuyến của (MNP) và (SAC) là PX.
d) Giao tuyến của (MNP) và (SAB) là MQ, với Q là giao điểm của AB và PX. Vì P thuộc SC, nên PX cắt SC tại X. Vì X thuộc AC, nên X thuộc (ABCD). Vì ABCD là hình bình hành, nên AC cắt AB tại một điểm, gọi là Q. Vì Q thuộc AB, nên Q thuộc (SAB). Vì Q thuộc PX, nên Q thuộc (MNP). Do đó, giao tuyến của (MNP) và (SAB) là đường thẳng đi qua M và Q. Vì M là trung điểm của SB, nên MQ chính là đường thẳng cần tìm. Vậy giao tuyến của (MNP) và (SAB) là MQ.
e) Giao tuyến của (MNP) và (SAD) là NY, với Y là giao điểm của AD và PX. Vì P thuộc SC, nên PX cắt SC tại X. Vì X thuộc AC, nên X thuộc (ABCD). Vì ABCD là hình bình hành, nên AC cắt AD tại một điểm, gọi là Y. Vì Y thuộc AD, nên Y thuộc (SAD). Vì Y thuộc PX, nên Y thuộc (MNP). Do đó, giao tuyến của (MNP) và (SAD) là đường thẳng đi qua N và Y. Vì N là trung điểm của SD, nên NY chính là đường thẳng cần tìm. Vậy giao tuyến của (MNP) và (SAD) là NY.
f) Giao tuyến của (MNP) và (ABCD) là XY. Vì X là giao điểm của NP và AC, và Y là giao điểm của NP và AD. Nên XY là đường thẳng đi qua X và Y. Vì X thuộc AC, nên X thuộc (ABCD). Vì Y thuộc AD, nên Y thuộc (ABCD). Do đó, giao tuyến của (MNP) và (ABCD) là XY.
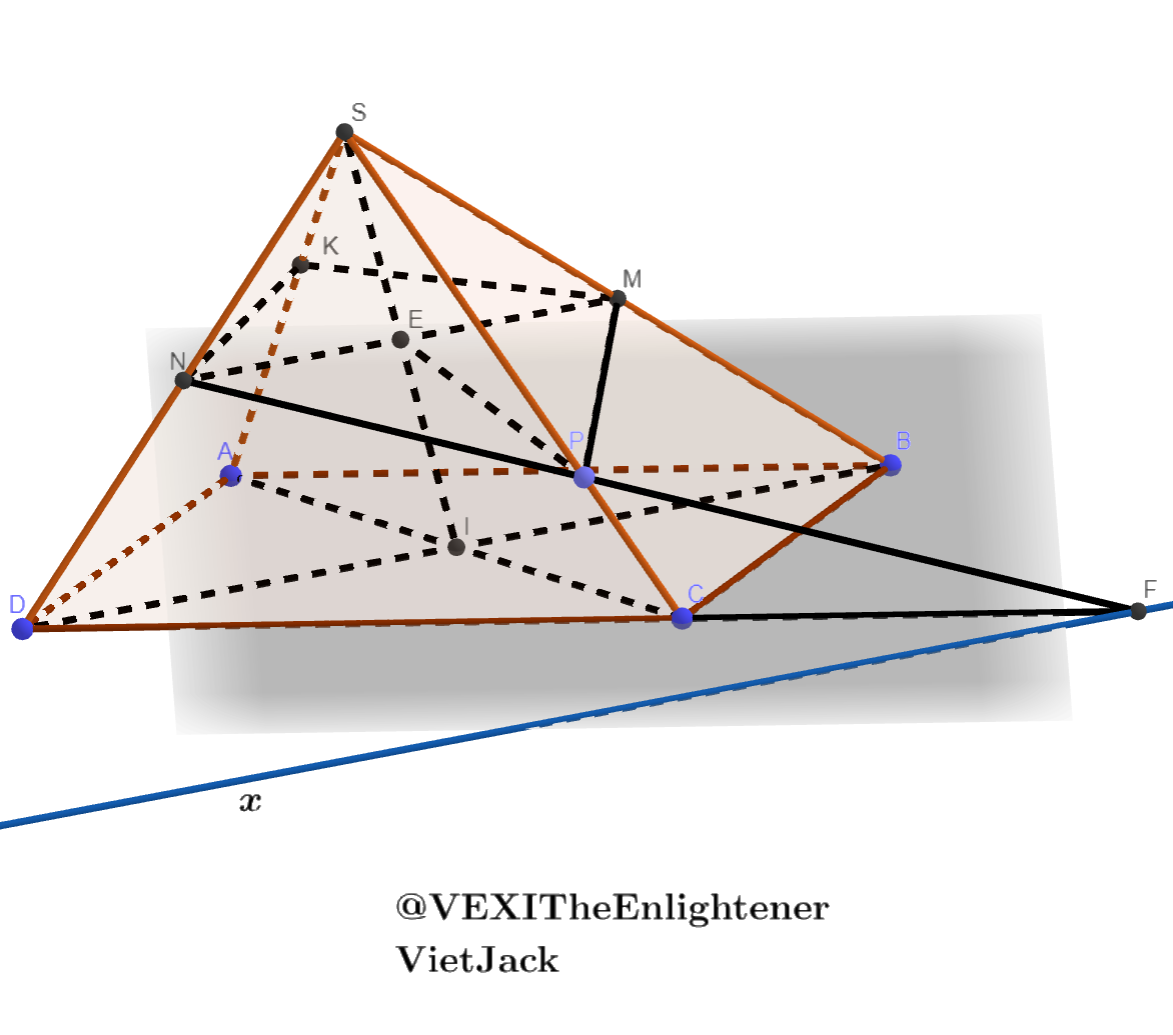
$\textbf{a}\bigg)$
Trong $(ABCD)$, gọi $I = AC \cap BD$
$\Rightarrow I \in (SAC) \cap (SBD)$
Mà $S \in (SAC) \cap (SBD)$
$\Rightarrow (SAC) \cap (SBD) = SI$
$\textbf{b}\bigg)$
Ta có: $\begin {cases} M \in (MNP) \\ M \in SB, SB \subset (SBD) \end {cases}$
$\Rightarrow M \in (SBD) \cap (MNP)$
Ta có: $\begin {cases} N \in (MNP) \\ N \in SD, SD \subset (SBD) \end {cases}$
$\Rightarrow N \in (SBD) \cap (MNP)$
$\Rightarrow (SBD) \cap (MNP) = MN$
$\textbf{c}\bigg)$
Trong $(SBD)$, gọi $E = SI \cap MN$
$\Rightarrow E \in (SAC) \cap (MNP)$
Ta có: $\begin {cases} N \in (MNP) \\ N \in SD, SD \subset (SAD) \end {cases}$
$\Rightarrow N \in (MNP) \cap (SAD)$
$\begin {cases} K \in SA, SA \subset (SAD) \\ K \in PE, PE \subset (MNP) \end {cases}$
$\Rightarrow K \in (MNP) \cap (SAD)$
kb
Quảng cáo
Bạn muốn hỏi bài tập?


