Cho hình vuông A'B'C'D' nằm trong hình vuông ABCD sao cho thứ tự các đỉnh theo cùng một chiều là như nhau (tức là nếu vẽ hai đường tròn, mỗi đường tròn qua các đỉnh của một hình vuông, thì chiều đi trên đường tròn từ A lần lượt qua B, C, D và từ A' lần lượt qua B', C', D' là như nhau). Chứng minh rằng trung điểm các đoạn thẳng AA', BB', CC', DD' là đỉnh của một hình vuông.
Quảng cáo
2 câu trả lời 257
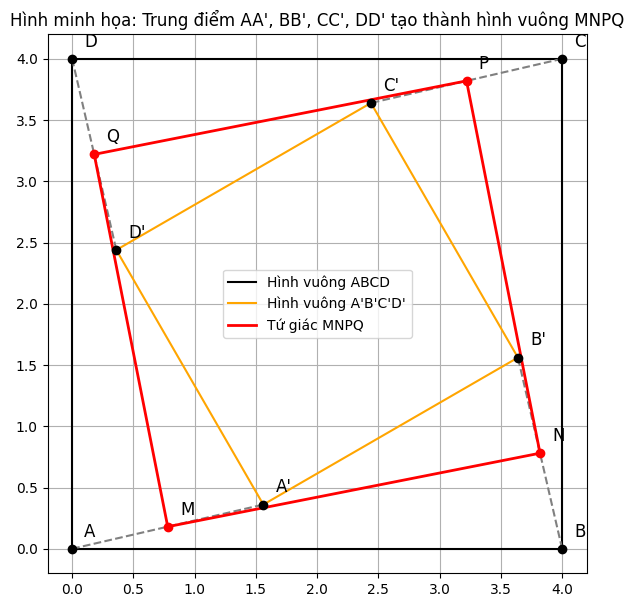 + Xét các đoạn nối trung điểm
+ Xét các đoạn nối trung điểm
M là trung điểm của AA′
N là trung điểm của BB′
P là trung điểm của CC′
Q là trung điểm của DD′
+ Chứng minh MNPQ là hình chữ nhật
Xét hai đoạn thẳng MN và PQ:
MN là đoạn nối trung điểm của AA′ và BB′
AA′ và BB′ là hai đoạn song song và bằng nhau (vì AA′BB′ là hình bình hành do phép quay bảo toàn tỉ lệ và góc)
⇒ Tứ giác AA′BB là hình bình hành, do đó đoạn nối hai trung điểm M và N sẽ:
Song song với AB
Bằng nửa tổng hai đường chéo nếu cần
Tương tự, PQ nối trung điểm của CC′ và DD′, mà CC′ // DD′, nên PQ // MN
⟹ MN // PQ
Tương tự, chứng minh được N nối với P song song và bằng với Q nối với M
⟹ Tứ giác MNPQ là hình bình hành có hai cặp cạnh đối song song và bằng nhau
+ Chứng minh MNPQ có góc vuông
Vì cả hai hình vuông ABCD và A′B′C′D′ đều có các góc vuông, nên các đoạn nối trung điểm tương ứng như MN và NP tạo thành góc vuông.
Vì phép quay bảo toàn góc và chiều, nên:
Góc giữa MN và NP bằng góc giữa AB và BC là 90∘
⟹ Tứ giác MNPQ là hình bình hành có một góc vuông
⟹ MNPQ là hình chữ nhật có góc vuông
Mà hình chữ nhật có các cạnh bằng nhau ⇒ là hình vuông.
Sau khi có tọa độ các trung điểm, ta tính độ dài các cạnh và kiểm tra tính vuông góc của các cạnh kề để chứng minh MNPQ là một hình vuông (ví dụ, kiểm tra độ dài MN, NP, PQ, QM và tích vô hướng của các vectơ chỉ phương của các cạnh kề).
Quảng cáo
Bạn muốn hỏi bài tập?


