Cho hình chóp S.ABCD có đáy ABCD là hình bình hành =.Gọi M,N là lượt là trung điểm của các cạnh BC,CD
a)Xác định giao tuyến của hai mặt phẳng (SAM) và (SCD)
b)Xác định giao tuyến của hai mặt phẳng (SBN) và (SAD)
c)Xác định giao tuyến của hai mặt phẳng (SAM) và (SBN)
Quảng cáo
3 câu trả lời 322
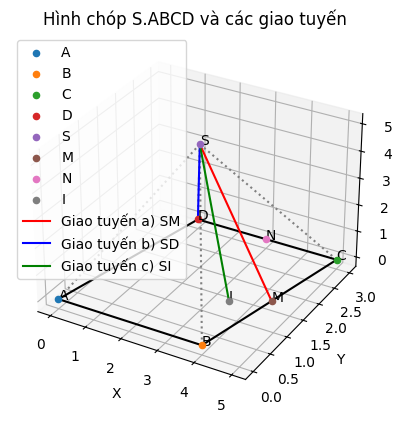
C ∈ mặt phẳng đáy , nhưng không thuộc mặt phẳng (SAM), nên xét theo hướng khác.
Xét điểm M ∈ BCM , mà M ∈ (SAM)
M là trung điểm của BC, nên C ∈ (SCD), M ∈ (SAM), đoạn thẳng MC nằm trong mặt phẳng (SCD).
Hai điểm M ∈ (SAM) ∩ (SCD)
Vậy : (SAM) ∩ (SCD) = SM
Lấy hai điểm chung:
S ∈ (SBN) ∩ (SAD)
D ∈ (SAD) , N là trung điểm của CD
⇒ DN ∈ (SBN) ∩ (SAD)
⇒ Giao tuyến là đường thẳng qua S và giao điểm của DN với mặt phẳng (SAD)
→ Hai điểm chung là S và I = DN ∩ SA
Xét đoạn thẳng SD, vì:
S ∈ (SBN) ∩ (SAD)
D ∈ (SAD), N ∈ CD ⊂ (SBN)
→ đoạn SD chứa hai điểm chung.
Vậy : (SBN) ∩ (SAD) = SD
M ∈ (SAM), M ∈ BCM
B ∈ (SBN) , C ∈ đáy, nên đoạn BC chứa cả B, M
→ M ∈ (SAM), B ∈ (SBN), BC nối hai điểm đó
⇒ đoạn MB nằm trên cạnh đáy
→ Hai mặt phẳng có thể cắt nhau theo đường thẳng qua S và điểm I = MB ∩ (cả hai mặt phẳng)
Xét điểm M thuộc BC, B thuộc (SBN)
⇒ đoạn thẳng MB thuộc không gian chung
⇒ lấy giao tuyến là SI với I là điểm bất kỳ trên MB
⇒ BC ∈ mặt đáy ⇒ có thể nằm trong giao nhau
→ Hai điểm chung: S và I = giao điểm của AM và BN nếu chúng cắt nhau
Vậy : (SAM) ∩ (SBN) = SI, trong đó I = AM ∩ BN
a) Giao tuyến của hai mặt phẳng (AMO) và (SCD)
Để xác định giao tuyến của hai mặt phẳng này, ta cần tìm hai điểm chung thuộc cả hai mặt phẳng.
Tìm điểm chung thứ nhất:
Theo đề bài, M là một điểm nằm trên cạnh SC.
Do đó, M thuộc mặt phẳng (SCD).
M cũng thuộc mặt phẳng (AMO).
Suy ra, M là điểm chung thứ nhất.
Tìm điểm chung thứ hai:
Ta xét hai đường thẳng nằm trong hai mặt phẳng và cắt nhau.
Trong mặt phẳng (AMO) có đường thẳng AO (đây là một phần của đường chéo AC của đáy).
Trong mặt phẳng (SCD) có đường thẳng CD.
Hai đường thẳng AO và CD đều nằm trong mặt phẳng đáy (ABCD) nên chúng đồng phẳng. Vì ABCD là một tứ giác lồi bất kỳ, đường chéo AC và cạnh CD sẽ cắt nhau tại một điểm.
Gọi E là giao điểm của AO và CD.
Vì E thuộc đường thẳng AO, nên E thuộc mặt phẳng (AMO).
Vì E thuộc đường thẳng CD, nên E thuộc mặt phẳng (SCD).
Suy ra, E là điểm chung thứ hai.
Kết luận: Giao tuyến của hai mặt phẳng (AMO) và (SCD) là đường thẳng ME.
b) Giao tuyến của hai mặt phẳng (BMO) và (SCD)
Tương tự câu a, ta cũng tìm hai điểm chung của hai mặt phẳng này.
Tìm điểm chung thứ nhất:
Theo đề bài, M là điểm thuộc cạnh SC.
Do đó, M thuộc mặt phẳng (SCD).
M cũng thuộc mặt phẳng (BMO).
Suy ra, M là điểm chung thứ nhất.
Tìm điểm chung thứ hai:
Ta xét hai đường thẳng nằm trong hai mặt phẳng và cắt nhau.
Trong mặt phẳng (BMO) có đường thẳng BO (một phần của đường chéo BD của đáy).
Trong mặt phẳng (SCD) có đường thẳng CD.
Hai đường thẳng BO và CD đều nằm trong mặt phẳng đáy (ABCD).
Gọi F là giao điểm của BO và CD.
Vì F thuộc đường thẳng BO, nên F thuộc mặt phẳng (BMO).
Vì F thuộc đường thẳng CD, nên F thuộc mặt phẳng (SCD).
Suy ra, F là điểm chung thứ hai.
Kết luận: Giao tuyến của hai mặt phẳng (BMO) và (SCD) là đường thẳng MF.
Hai mặt phẳng (SAM) và (SCD) có điểm chung S.
2. Điểm chung thứ hai:
Kéo dài AM cắt DC tại E.
Điểm E thuộc DC nên E thuộc mặt phẳng (SCD).
Điểm E thuộc AM nên E thuộc mặt phẳng (SAM).
Vậy E là điểm chung thứ hai của hai mặt phẳng (SAM) và (SCD).
3. Giao tuyến:
Giao tuyến của (SAM) và (SCD) là đường thẳng SE.
b) Xác định giao tuyến của hai mặt phẳng (SBN) và (SAD)
1. Điểm chung thứ nhất:
Hai mặt phẳng (SBN) và (SAD) có điểm chung S.
2. Điểm chung thứ hai:
Kéo dài BN cắt AD tại F.
Điểm F thuộc AD nên F thuộc mặt phẳng (SAD).
Điểm F thuộc BN nên F thuộc mặt phẳng (SBN).
Vậy F là điểm chung thứ hai của hai mặt phẳng (SBN) và (SAD).
3. Giao tuyến:
Giao tuyến của (SBN) và (SAD) là đường thẳng SF.
c) Xác định giao tuyến của hai mặt phẳng (SAM) và (SBN)
1. Điểm chung thứ nhất:
Hai mặt phẳng (SAM) và (SBN) có điểm chung S.
2. Điểm chung thứ hai:
Trong mặt phẳng (ABCD), gọi I là giao điểm của AM và BN.
Điểm I thuộc AM nên I thuộc mặt phẳng (SAM).
Điểm I thuộc BN nên I thuộc mặt phẳng (SBN).
Vậy I là điểm chung thứ hai của hai mặt phẳng (SAM) và (SBN).
3. Giao tuyến:
Giao tuyến của (SAM) và (SBN) là đường thẳng SI.
Quảng cáo
Bạn muốn hỏi bài tập?


