Cho hình chóp S.ABCD. Gọi O là giao điểm của AC và BD và gọi M là một điểm bất kì thuộc cạnh SC
a)Xác định giao tuyến của hai mặt phẳng (AMO) và (SCD)
b)Xác định giao tuyến của hai mặt phẳng(BMO) và (SCD)
Quảng cáo
3 câu trả lời 194
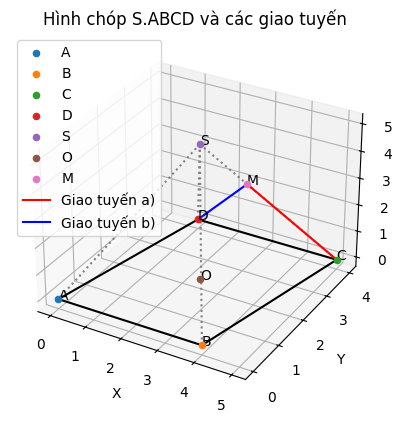
a) Xác định giao tuyến của hai mặt phẳng (AMO) và (SCD)
+ Phân tích:
Mặt phẳng (AMO) chứa 3 điểm không thẳng hàng: A,M,O
Mặt phẳng (SCD) chứa 3 điểm không thẳng hàng: S,C,D
=> Điểm chung dễ thấy đầu tiên là: M ∈ SC ⇒ M ∈ (SCD) và M cũng nằm trong (AMO)
→ M ∈ (AMO) ∩ (SCD)
=> Ta cần tìm thêm một điểm thứ hai thuộc cả hai mặt phẳng để xác định giao tuyến.
Xét đoạn AO(nằm trong (AMO))
Xét đoạn CD (nằm trong (SCD))
→ Nếu AO ∩ CD = I, thì đường thẳng MI chính là giao tuyến.
Vậy : Giao tuyến của hai mặt phẳng (AMO) và (SCD) là đường thẳng MI,
với I = AO ∩ CD
b) Xác định giao tuyến của hai mặt phẳng (BMO) và (SCD)
+ Phân tích:
Mặt phẳng (BMO): chứa B,M,O
Mặt phẳng (SCD): chứa S,C,D
=> M ∈ SC ⇒ M ∈ (SCD) và cũng là điểm trong (BMO)
→ M ∈ (BMO) ∩ (SCD)
=> Tìm thêm điểm thứ hai:
Xét đoạn BO ⊂ (BMO)
Xét đoạn CD ⊂ (SCD)
→ Nếu BO ∩ CD = J, thì đường thẳng MJ là giao tuyến.
Vậy : Giao tuyến của hai mặt phẳng (BMO) và (SCD) là đường thẳng MJ,
với J = BO ∩ CD
a) Giao tuyến của hai mặt phẳng (AMO) và (SCD)
Để xác định giao tuyến của hai mặt phẳng này, ta cần tìm hai điểm chung thuộc cả hai mặt phẳng.
Tìm điểm chung thứ nhất:
Theo đề bài, M là một điểm nằm trên cạnh SC.
Do đó, M thuộc mặt phẳng (SCD).
M cũng thuộc mặt phẳng (AMO).
Suy ra, M là điểm chung thứ nhất.
Tìm điểm chung thứ hai:
Ta xét hai đường thẳng nằm trong hai mặt phẳng và cắt nhau.
Trong mặt phẳng (AMO) có đường thẳng AO (đây là một phần của đường chéo AC của đáy).
Trong mặt phẳng (SCD) có đường thẳng CD.
Hai đường thẳng AO và CD đều nằm trong mặt phẳng đáy (ABCD) nên chúng đồng phẳng. Vì ABCD là một tứ giác lồi bất kỳ, đường chéo AC và cạnh CD sẽ cắt nhau tại một điểm.
Gọi E là giao điểm của AO và CD.
Vì E thuộc đường thẳng AO, nên E thuộc mặt phẳng (AMO).
Vì E thuộc đường thẳng CD, nên E thuộc mặt phẳng (SCD).
Suy ra, E là điểm chung thứ hai.
Kết luận: Giao tuyến của hai mặt phẳng (AMO) và (SCD) là đường thẳng ME.
b) Giao tuyến của hai mặt phẳng (BMO) và (SCD)
Tương tự câu a, ta cũng tìm hai điểm chung của hai mặt phẳng này.
Tìm điểm chung thứ nhất:
Theo đề bài, M là điểm thuộc cạnh SC.
Do đó, M thuộc mặt phẳng (SCD).
M cũng thuộc mặt phẳng (BMO).
Suy ra, M là điểm chung thứ nhất.
Tìm điểm chung thứ hai:
Ta xét hai đường thẳng nằm trong hai mặt phẳng và cắt nhau.
Trong mặt phẳng (BMO) có đường thẳng BO (một phần của đường chéo BD của đáy).
Trong mặt phẳng (SCD) có đường thẳng CD.
Hai đường thẳng BO và CD đều nằm trong mặt phẳng đáy (ABCD).
Gọi F là giao điểm của BO và CD.
Vì F thuộc đường thẳng BO, nên F thuộc mặt phẳng (BMO).
Vì F thuộc đường thẳng CD, nên F thuộc mặt phẳng (SCD).
Suy ra, F là điểm chung thứ hai.
Kết luận: Giao tuyến của hai mặt phẳng (BMO) và (SCD) là đường thẳng MF.
M là điểm chung của (AMO) và (SCD) vì M thuộc SC và SC nằm trong (SCD), đồng thời M cũng thuộc (AMO).
2. Tìm điểm chung thứ hai:
Trong mặt phẳng (ABCD), gọi I là giao điểm của AO và CD.
Vì AO nằm trong (AMO) và CD nằm trong (SCD), nên I là điểm chung thứ hai của (AMO) và (SCD).
3. Kết luận:
Giao tuyến của hai mặt phẳng (AMO) và (SCD) là đường thẳng MI.
b) Xác định giao tuyến của hai mặt phẳng (BMO) và (SCD)
1. Tìm điểm chung thứ nhất:
M là điểm chung của (BMO) và (SCD) vì M thuộc SC và SC nằm trong (SCD), đồng thời M cũng thuộc (BMO).
2. Tìm điểm chung thứ hai:
Trong mặt phẳng (ABCD), gọi K là giao điểm của BO và CD.
Vì BO nằm trong (BMO) và CD nằm trong (SCD), nên K là điểm chung thứ hai của (BMO) và (SCD).
3. Kết luận:
Giao tuyến của hai mặt phẳng (BMO) và (SCD) là đường thẳng MK.
Quảng cáo
Bạn muốn hỏi bài tập?


