Cho tam giác ABC, các đường cao BD, CE cắt nhau tại H. Đường vuông góc với AB tại B và đường vuông góc với AC tại C cắt nhau ở K. Gọi M là trung điểm của BC
a.CM AH vuông góc với BC
b.CM tứ giác BHCK là hình bình hành
Quảng cáo
3 câu trả lời 193
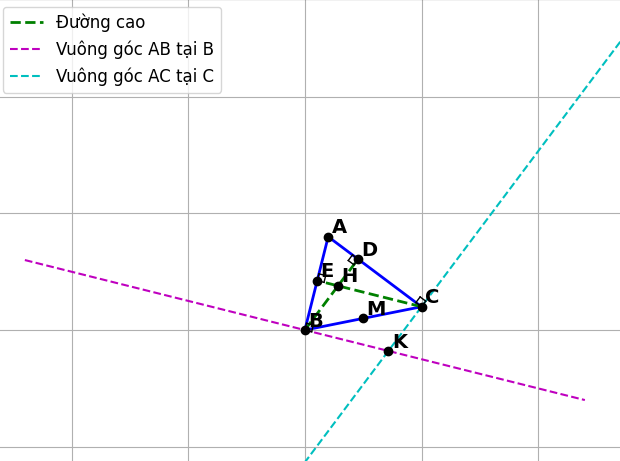
a) Chứng minh AH ⊥ BC
BD và CE là các đường cao của tam giác ABC, do đó BD ⊥ AC và CE ⊥ AB.
H là giao điểm của hai đường cao BD và CE, nên H là trực tâm của tam giác ABC.
=> AH ⊥ BC (tính chất trong tam giác: Đường thẳng nối đỉnh A và trực tâm H vuông góc với đường thẳng BC).
Vậy AH ⊥ BC (đpcm).
K là giao điểm của hai đường thẳng:
Đường vuông góc với AB tại B (gọi là l1)
Đường vuông góc với AC tại C (gọi là l2)
+ BH là một phần của đường cao BD, và BD ⊥ AC.
Đường l2 (vuông góc với AC tại C) đi qua K, vậy CK ⊥ AC.
Do BD ⊥ AC và CK ⊥ AC, hai đoạn thẳng BD (và đoạn BH ⊂ BD) và CK đều vuông góc với AC, nên BH // CK
+ BC là cạnh đáy tam giác.
l1 (đường vuông góc với AB tại B) đi qua B và K.
CE ⊥ AB(đường cao CE vuông góc với AB).
CE và l1 đều vuông góc với AB nên song song với nhau.
Vì H ∈ CE và K ∈ l1, suy ra HK // BC.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
9895
Đã trả lời bởi chuyên gia
9895 -
 Đã trả lời bởi chuyên gia
7691
Đã trả lời bởi chuyên gia
7691


