Cho hình bình hành ABCD. Gọi O là giao điểm AC, BD. Trên AB lấy E, trên CĐ lấy F...

· 15:32 07/08/2025

Chương 1: Tứ giác

Cho hình bình hành ABCD. Gọi O là giao điểm AC, BD. Trên AB lấy E, trên CĐ lấy F sao cho AE = CF.
a) CMR: O là trung điểm của EF.
b) Từ E kẻ Ex//AC cắt BC tại I. Từ F kẻ Fy//AC cắt AD tại K. CMR: EI = FK
c) CMR: O là trung điểm của IK.
Giúp mình với mình đang vội !

Trả Lời (+5 điểm)

Hỏi chi tiết

Quảng cáo

3 câu trả lời 641

Gia Hân

4 tháng trước

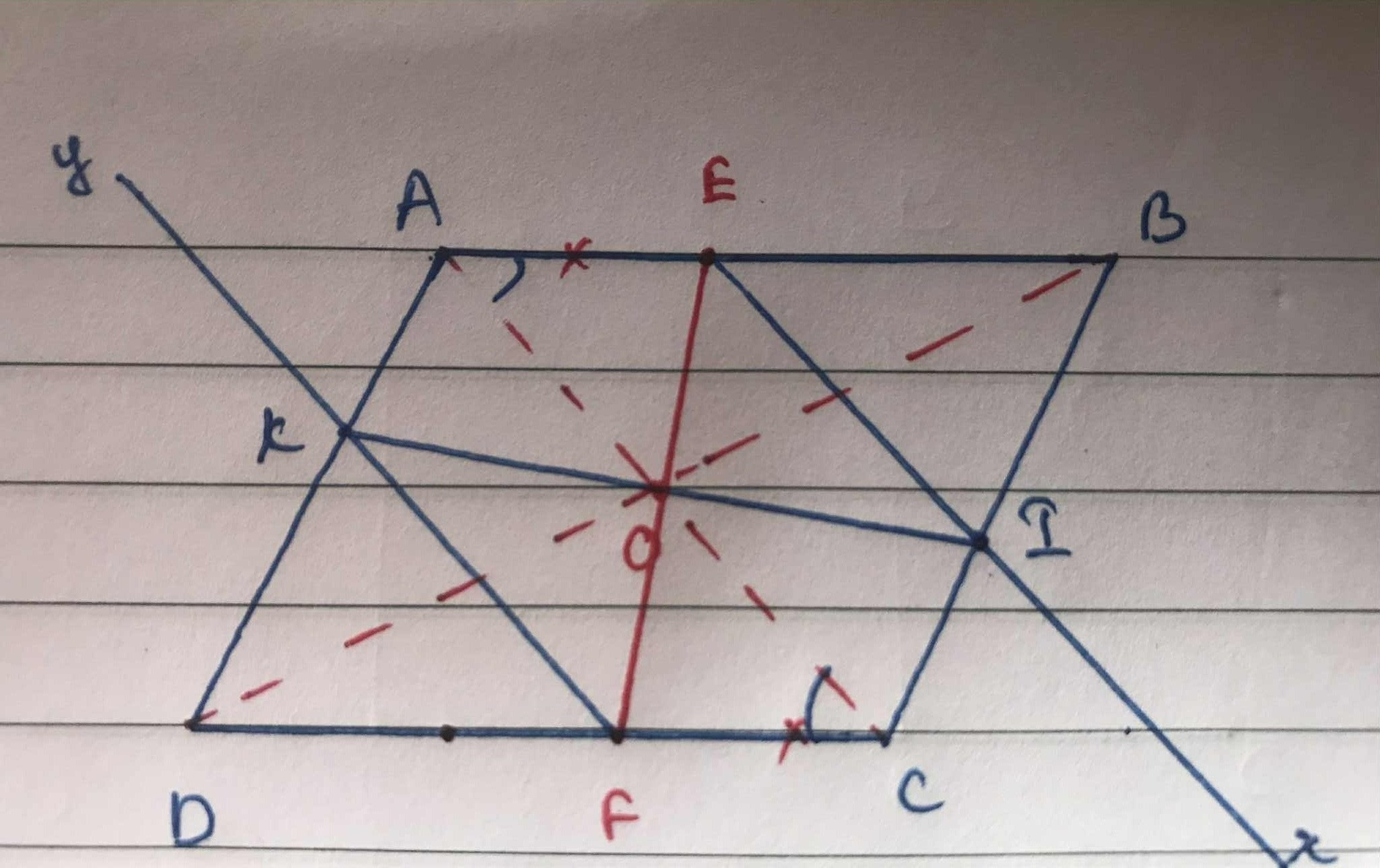Hỏi đáp VietJack a) Chứng minh O là trung điểm của EF

Xét hai tam giác △AOE và △COF.
Ta có: AO = OC (O là trung điểm AC).

\hat{E A O}

\hat{F C O}

(hai góc so le trong do AB // CD và AC là cát tuyến).
AE=CF (theo giả thiết).
=> △AOE = △COF (c.g.c).

=> EO = OF (hai cạnh tương ứng).
Vì EO = OF và E, O, F thẳng hàng (vì O thuộc AC, E thuộc AB, F thuộc CD, và xét tam giác AOE và COF, do tính đối xứng qua O), nên O là trung điểm của đoạn thẳng EF.

b) Xét △AEI và △CFK có:

\hat{A E I}

\hat{C F K}

cùng có một cặp góc đồng vị (do cùng song song với AC)

AE = CF (giả thiết)

Góc tại đỉnh A = góc tại đỉnh C (do ABCD là hình bình hành)

=> △AEI = △CFK

=> EI = FK (hai cạnh tương ứng)

c) Xét đoạn thẳng IK nối từ I đến K

có : EI = FK và EI // FK (cùng // AC) ⇒ tứ giác EFKI là hình bình hành

Trong hình bình hành:

Giao điểm hai đường chéo là trung điểm của mỗi đường chéo

Mà O là trung điểm của EF (phần a)

⇒ O cũng là trung điểm của IK (đpcm)

...Xem thêm

0 bình luận

1 ( 5.0 )

Đăng nhập để hỏi chi tiết

Dương Công Minh

4 tháng trước

0 bình luận

Đăng nhập để hỏi chi tiết

An mê otp Dương Hùng.

4 tháng trước

a) Chứng minh O là trung điểm của EF:
Chứng minh:Xét tứ giác AECF có: AE // CF (vì AB // CD) và AE = CF (gt)
=> AECF là hình bình hành (dhnb)
=> AC và EF cắt nhau tại trung điểm của mỗi đường (tính chất hình bình hành)
Mà O là trung điểm của AC (O là giao điểm của AC và BD trong hình bình hành ABCD)
=> O là trung điểm của EF (đpcm)
b) Chứng minh EI = FK:
Chứng minh:Xét tam giác AEI có: Ex // AC (gt)
=> EIAC=BEABACEI=ABBE (định lý Ta-lét)
Tương tự, xét tam giác CFK có: Fy // AC (gt)
=> FKAC=DFCDACFK=CDDF (định lý Ta-lét)
Mà AE = CF (gt) => BE = DF (vì AB = CD)
=> BEAB=DFCDABBE=CDDF
=> EIAC=FKACACEI=ACFK
=> EI = FK (đpcm)
c) Chứng minh O là trung điểm của IK:
Chứng minh:Gọi M là giao điểm của EI và BD, N là giao điểm của FK và BD.
Xét tam giác BME có: EI // AC (Ex // AC)
=> BMBO=BEBABOBM=BABE (định lý Ta-lét)
Tương tự, xét tam giác DNF có: FK // AC (Fy // AC)
=> DNDO=DFDCDODN=DCDF (định lý Ta-lét)
Mà BE = DF (cmt) và BA = DC (tính chất hình bình hành)
=> BEBA=DFDCBABE=DCDF
=> BMBO=DNDOBOBM=DODN
Mà BO = DO (O là trung điểm của BD)
=> BM = DN
=> M là trung điểm của EI và N là trung điểm của FK (vì EI // AC // FK)
Xét tứ giác EIFK có: EI // FK (cùng song song với AC) và EI = FK (cmt)
=> EIFK là hình bình hành (dhnb)
=> EF và IK cắt nhau tại trung điểm của mỗi đường (tính chất hình bình hành)
Mà O là trung điểm của EF (cmt)
=> O là trung điểm của IK (đpcm)

...Xem thêm

0 bình luận

1 ( 5.0 )

Đăng nhập để hỏi chi tiết

Quảng cáo

Bạn muốn hỏi bài tập?