Question

Đã trả lời bởi chuyên gia

Answer 1

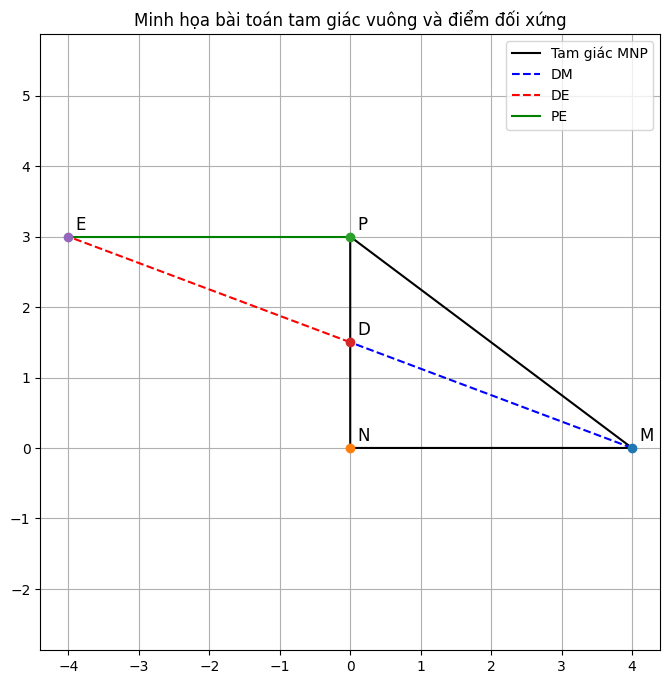
Hỏi đáp VietJack

+ Ta có : D là trung điểm của NP ⇒ DN = DP
E được lấy đối xứng qua D theo đoạn DM, do DE = DM và E nằm trên tia đối của tia DM
⟹ Tam giác MDE là tam giác cân tại D, với DE = DM

⟹ E là ảnh đối xứng của M qua điểm D

Do đó: EM = 2.DM

+ Ta xét các đoạn:

Tam giác △MNP vuông tại N
D là trung điểm của NP
Từ đó: đường trung tuyến từ đỉnh vuông M tới cạnh NP, có chiều dài bằng nửa cạnh huyền MN

Trong tam giác vuông MNP vuông tại N:

Định lý: Trung tuyến từ đỉnh M tới trung điểm D của cạnh NP sẽ có độ dài bằng nửa cạnh huyền MP.
⟹ MD = $\frac{1}{2}$ MP

Mà DE = DM ⇒ PE = 2⋅DM = MP

⇒ PE = MP = MN (đpcm)

+ So sánh PE với MD:
PE = 2⋅DM
Vậy: PE = 2⋅MD

Answer 2

a) Chứng minh MN = PE. So sánh PE với MD

Các bước làm:

Xét hai tam giác: Xét △MND và △EPD.
Chứng minh hai tam giác bằng nhau:

Sử dụng giả thiết D là trung điểm của NP để suy ra ND=DP.
Sử dụng giả thiết DE=DM.
Sử dụng hai góc đối đỉnh ∠MDN và ∠EDP.
Kết luận △MND=△EPD (cạnh - góc - cạnh).
Suy ra các yếu tố tương ứng:

Từ hai tam giác bằng nhau, suy ra hai cạnh tương ứng bằng nhau là MN=PE.
Vì DE=DM theo giả thiết, và E thuộc tia đối của tia DM, nên MD và DE nằm trên một đường thẳng. Do đó, ME=MD+DE=MD+MD=2MD.
So sánh PE với MD:

Do △MND=△EPD, suy ra MN=PE và MD=DE.
Theo giả thiết, E trên tia đối của tia DM và DE=DM. Vì vậy ME=2MD.
Xét hai tam giác bằng nhau, ta có các cạnh tương ứng bằng nhau, nhưng không thể trực tiếp so sánh PE với MD từ đây.
Tuy nhiên, ta đã có MN=PE.
Đáp án:

Chứng minh MN = PE: Xét △MND và △EPD có:

ND=DP (vì D là trung điểm của NP)
∠MDN=∠EDP (hai góc đối đỉnh)
DM=DE (theo giả thiết) Vậy △MND=△EPD (c.g.c). ⟹MN=PE (hai cạnh tương ứng).
So sánh PE với MD: Trong △MNP có ∠N=90∘, MN là cạnh góc vuông, MD là đường trung tuyến ứng với cạnh huyền MP của tam giác vuông MNP. MN và MP là hai cạnh khác nhau, do đó không thể suy ra mối quan hệ trực tiếp giữa MN và MD (từ đó so sánh PE với MD). Tuy nhiên, ta đã có MN=PE. Do đó, không có mối quan hệ trực tiếp giữa PE và MD mà có thể so sánh được trong bài toán này.

...Xem thêm

Answer 3

a) Chứng minh MN = PE. So sánh PE với MD

Các bước làm:

Xét hai tam giác: Xét △MND và △EPD.
Chứng minh hai tam giác bằng nhau:

Sử dụng giả thiết D là trung điểm của NP để suy ra ND=DP.
Sử dụng giả thiết DE=DM.
Sử dụng hai góc đối đỉnh ∠MDN và ∠EDP.
Kết luận △MND=△EPD (cạnh - góc - cạnh).
Suy ra các yếu tố tương ứng:

Từ hai tam giác bằng nhau, suy ra hai cạnh tương ứng bằng nhau là MN=PE.
Vì DE=DM theo giả thiết, và E thuộc tia đối của tia DM, nên MD và DE nằm trên một đường thẳng. Do đó, ME=MD+DE=MD+MD=2MD.
So sánh PE với MD:

Do △MND=△EPD, suy ra MN=PE và MD=DE.
Theo giả thiết, E trên tia đối của tia DM và DE=DM. Vì vậy ME=2MD.
Xét hai tam giác bằng nhau, ta có các cạnh tương ứng bằng nhau, nhưng không thể trực tiếp so sánh PE với MD từ đây.
Tuy nhiên, ta đã có MN=PE.
Đáp án:

Chứng minh MN = PE: Xét △MND và △EPD có:

ND=DP (vì D là trung điểm của NP)
∠MDN=∠EDP (hai góc đối đỉnh)
DM=DE (theo giả thiết) Vậy △MND=△EPD (c.g.c). ⟹MN=PE (hai cạnh tương ứng).
So sánh PE với MD: Trong △MNP có ∠N=90∘, MN là cạnh góc vuông, MD là đường trung tuyến ứng với cạnh huyền MP của tam giác vuông MNP. MN và MP là hai cạnh khác nhau, do đó không thể suy ra mối quan hệ trực tiếp giữa MN và MD (từ đó so sánh PE với MD). Tuy nhiên, ta đã có MN=PE. Do đó, không có mối quan hệ trực tiếp giữa PE và MD mà có thể so sánh được trong bài toán này.

Answer 4

a) Chứng minh MN = PE. So sánh PE với MD

Các bước làm:

Xét hai tam giác: Xét △MND và △EPD.
Chứng minh hai tam giác bằng nhau:

Sử dụng giả thiết D là trung điểm của NP để suy ra ND=DP.
Sử dụng giả thiết DE=DM.
Sử dụng hai góc đối đỉnh ∠MDN và ∠EDP.
Kết luận △MND=△EPD (cạnh - góc - cạnh).
Suy ra các yếu tố tương ứng:

Từ hai tam giác bằng nhau, suy ra hai cạnh tương ứng bằng nhau là MN=PE.
Vì DE=DM theo giả thiết, và E thuộc tia đối của tia DM, nên MD và DE nằm trên một đường thẳng. Do đó, ME=MD+DE=MD+MD=2MD.
So sánh PE với MD:

Do △MND=△EPD, suy ra MN=PE và MD=DE.
Theo giả thiết, E trên tia đối của tia DM và DE=DM. Vì vậy ME=2MD.
Xét hai tam giác bằng nhau, ta có các cạnh tương ứng bằng nhau, nhưng

3 câu trả lời 113

Câu hỏi hot cùng chủ đề

Bài viết mới nhất Lớp 7