Quảng cáo
3 câu trả lời 153
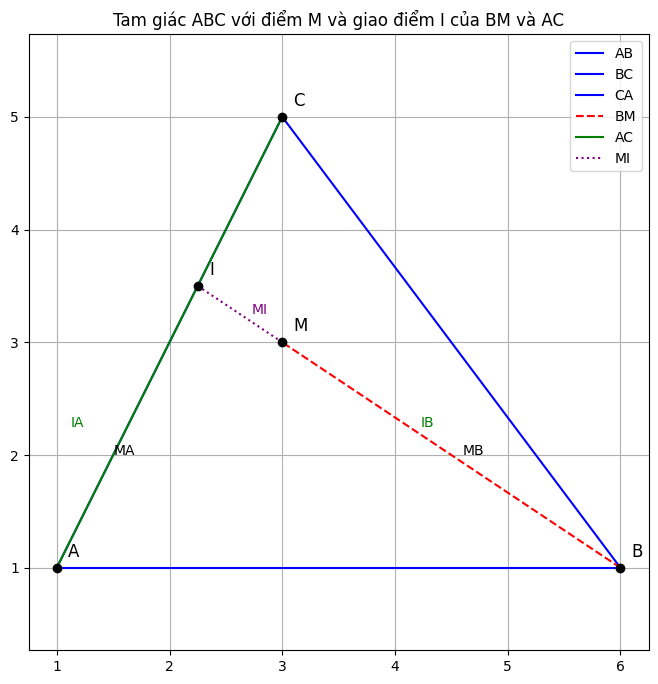
a) Xét tam giác AMI: vì M nằm trong tam giác nên M ≠ I.
Theo bất đẳng thức tam giác:
MA + MI > IA ⇒MA > IA − MI
Tương tự với tam giác BMI:
MB + MI > IB ⇒ MB > IB − MI
Cộng hai bất đẳng thức:
MA + MB > (IA − MI) + (IB − MI) = IA + IB − 2MI , MI > 0
→ nên: MA + MB > IA + IB − 2MI
Vì 2MI > 0, ta có:
MA + MB < IA + IB
Vậy : MA + MB < IA + IB (đpcm)
b)
Vì I nằm trên đoạn AC, nên:
AI + IC = AC
Dùng ý a), ta có: MA + MB < IA + IB
Mặt khác, IB là khoảng cách từ I đến B, IB ≤ IC + CB (bất đẳng thức tam giác trong tam giác ICB):
Thay vào:
MA + MB < IA + IB ≤ IA + IC + CB = AC + BC
Vậy : MA + MB < AC + BC (đpcm)
Bài toán này có vẻ như có một chút nhầm lẫn ở câu a). Với các điểm đã cho, không thể chứng minh MA+MB<IA+IB. Thay vào đó, ta có thể chứng minh IA+IB<MA+MB hoặc MA+MB<CA+CB.
Tuy nhiên, tôi sẽ giải quyết bài toán theo ý tưởng gốc là chứng minh quan hệ giữa các tổng đoạn thẳng. Tôi sẽ làm rõ mối quan hệ đúng đắn giữa các đoạn thẳng trong hình.
a) Chứng minh MA+MB<IA+IB
Để giải quyết câu này, ta cần xem xét lại vị trí của các điểm. Vì I là giao điểm của đường thẳng BM và AC, nên B, M, I là ba điểm thẳng hàng. Theo hình vẽ, M nằm giữa B và I.
Do đó, ta có: BI=BM+MI.
Xét tam giác AMI. Theo bất đẳng thức tam giác, ta luôn có: MA<IA+MI
Cộng BM vào cả hai vế của bất đẳng thức trên, ta được: MA+BM<IA+MI+BM
Vì MI+BM=BI, nên bất đẳng thức trở thành: MA+BM<IA+BI
Kết luận: MA+BM<IA+BI.
b) Chứng minh MA+MB<AC+BC
Để chứng minh bất đẳng thức này, ta sẽ áp dụng bất đẳng thức tam giác cho các tam giác nhỏ hơn.
Xét tam giác BIC: Theo bất đẳng thức tam giác, ta có: BI<BC+CI
Mặt khác, ta có I nằm giữa A và C, nên AC=AI+IC. Vậy CI=AC−AI.
Thay CI vào bất đẳng thức trên, ta được: BI<BC+(AC−AI) BI<AC+BC−AI
Vì I,M,B thẳng hàng và M nằm giữa I và B nên BI=BM+MI. Từ đó, bất đẳng thức trở thành: BM+MI<AC+BC−AI (1)
Xét tam giác AMI: Theo bất đẳng thức tam giác, ta có: AM<AI+MI (2)
Cộng vế với vế của (1) và (2), ta có: (BM+MI)+AM<(AC+BC−AI)+(AI+MI) BM+AM+MI<AC+BC+MI
Triệt tiêu MI ở cả hai vế, ta được: MA+MB<AC+BC
Kết luận: MA+MB<AC+BC.
a) MA + MB < IA + IB
1. Trong tam giác AIM, theo bất đẳng thức tam giác, ta có: MA<AI+IMc
.2. Ta có MB=MI+IB
.3. Cộng hai bất đẳng thức trên: MA+MB<(AI+IM)+(MI+IB)
.4. Rút gọn: MA+MB<AI+2IM+IB
.5. Vì IM>0c
, nên 2IM>02
. Do đó, AI+2IM+IB>AI+IB
.6. Suy ra: MA+MB<IA+IB
. b) MA + MB < AC + BC
1. Từ phần a), ta có MA+MB<IA+IB
2. Trong tam giác IBC, theo bất đẳng thức tam giác, ta có: IB<IC+BC
3. Thay thế IB
vào bất đẳng thức từ bước 1: MA+MB<IA+(IC+BC)
.4. Gộp các đoạn thẳng trên cạnh AC: MA+MB<(IA+IC)+BC
.5. Vì I nằm trên AC, nên IA+IC=AC
6. Suy ra: MA+MB<AC+BC
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120761
-
81498
-
59515


