a, Gọi M là trung điểm của BC

⇒ MB = MC

Xét các tam giác △ABM và △ACM

 a) Cho biết AB < AC. Chứng minh: ∠MAC<∠MAB

Để giải quyết bài toán này, ta sẽ sử dụng một phép dựng hình phụ.

Dựng hình: Từ điểm A, ta kéo dài đoạn thẳng AM đến điểm D sao cho M là trung điểm của AD.
Khi đó, tứ giác ABDC có hai đường chéo BC và AD cắt nhau tại trung điểm M của mỗi đường. Do đó, ABDC là một hình bình hành.
Từ tính chất của hình bình hành, ta có:

AB=CD
AC=BD
∠BAM=∠CDM (hai góc so le trong)
Xét △ACD:

Ta có các cạnh là AC, CD, AD.
Theo giả thiết, AB<AC. Mà AB=CD, nên ta có CD<AC.
Theo định lý về quan hệ giữa cạnh và góc đối diện trong một tam giác, cạnh nhỏ hơn thì đối diện với góc nhỏ hơn. Do đó, ∠CAD<∠ADC.
Kết nối các góc:

∠CAD chính là ∠MAC.
∠ADC chính là ∠CDM.
Mà ∠CDM=∠BAM.
Từ đó, ta có ∠MAC<∠BAM.
Kết luận: Vậy, nếu AB<AC thì ∠MAC<∠BAM.

b) Cho biết ∠MAC<∠BAM. Chứng minh: AB < AC

Đây là bài toán ngược lại của câu a). Ta sử dụng cách dựng hình tương tự.

Dựng hình: Kéo dài AM đến điểm D sao cho M là trung điểm của AD. ABDC là hình bình hành.
Từ tính chất của hình bình hành, ta có:

AB=CD
AC=BD
∠BAM=∠CDM
Theo giả thiết, ta có ∠MAC<∠BAM.
Kết nối các góc:

∠MAC chính là ∠CAD.
∠BAM=∠CDM=∠ADC.
Vậy ta có ∠CAD<∠ADC.
Xét △ACD:

Theo định lý về quan hệ giữa cạnh và góc đối diện, cạnh đối diện với góc nhỏ hơn thì nhỏ hơn.
Cạnh đối diện với ∠CAD là CD.
Cạnh đối diện với ∠ADC là AC.
Vì ∠CAD<∠ADC, ta suy ra CD<AC.
Kết nối các cạnh:

Mà CD=AB.
Từ đó, ta có AB<AC.
Kết luận: Vậy, nếu ∠MAC<∠BAM thì AB<AC.

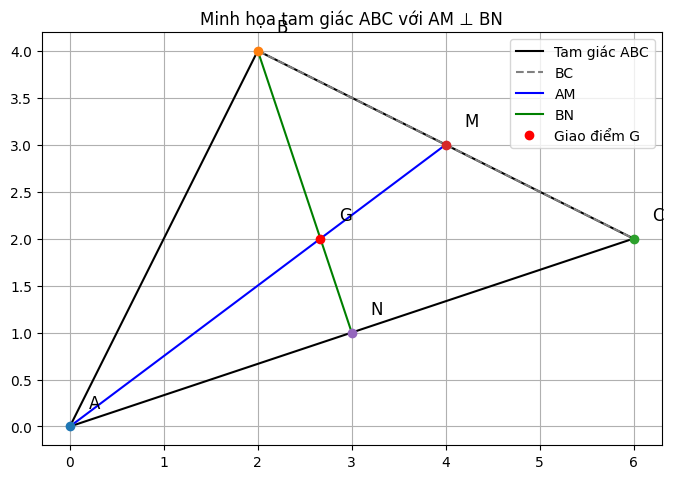
c) Gọi N là trung điểm của AC, AM cắt BN tại G. Cho biết AM⊥BN. Chứng minh: BC < 2AC

Phân tích: AM và BN là hai trung tuyến của tam giác ABC. G là giao điểm của hai trung tuyến nên G là trọng tâm của tam giác ABC.
Tính chất trọng tâm: G chia mỗi trung tuyến thành hai phần, trong đó đoạn thẳng từ đỉnh đến trọng tâm bằng 2/3 độ dài trung tuyến, và đoạn thẳng từ trọng tâm đến trung điểm cạnh đối diện bằng 1/3 độ dài trung tuyến.

BG=32​BN và GN=31​BN
AG=32​AM và GM=31​AM
Xét các tam giác vuông: Theo giả thiết, AM⊥BN tại G. Điều này có nghĩa là các tam giác △AGN, △BGM, △AGB và △NGM đều là các tam giác vuông tại G.
Áp dụng định lý Pytago:

Trong △BGM vuông tại G, ta có: BM2=BG2+GM2
Trong △AGN vuông tại G, ta có: AN2=AG2+GN2
Thay thế các giá trị:

BM2=(32​BN)2+(31​AM)2=94​BN2+91​AM2
AN2=(32​AM)2+(31​BN)2=94​AM2+91​BN2
So sánh BM và AC:

Ta biết rằng BC=2BM (vì M là trung điểm của BC) và AC=2AN (vì N là trung điểm của AC).
Ta sẽ so sánh BM2 và AN2.
AN2−BM2=(94​AM2+91​BN2)−(94​BN2+91​AM2)=93​AM2−93​BN2=31​(AM2−BN2)
Từ đó, ta thấy AN2−BM2 không thể giúp ta so sánh trực tiếp. Ta thử một cách khác.
Sử dụng trực tiếp các cạnh:

Ta có: AN2=94​AM2+91​BN2
BM2=91​AM2+94​BN2
AC2=(2AN)2=4AN2=4(94​AM2+91​BN2)=916​AM2+94​BN2
BM2=91​AM2+94​BN2
Ta thấy: AC2=915​AM2+91​AM2+94​BN2=915​AM2+BM2
Kết luận:

AC2=BM2+915​AM2.
Vì AM là độ dài một trung tuyến nên AM>0. Do đó, 915​AM2>0.
Suy ra AC2>BM2.
Vì AC và BM là các độ dài nên chúng dương, suy ra AC>BM.
Mà BM=21​BC, nên AC>21​BC.
Nhân cả hai vế với 2, ta được 2AC>BC, hay BC<2AC.
Kết luận: Vậy, nếu AM⊥BN thì BC<2AC.