Bài 5: Cho điểm A cách đường thẳng xy là 12cm. Vẽ đường tròn .(A,13cm)
a, Chứng minh (A) có hai giao điểm với xy.
b, Gọi hai giao điểm là B và C. Tính BC.
Quảng cáo
3 câu trả lời 237
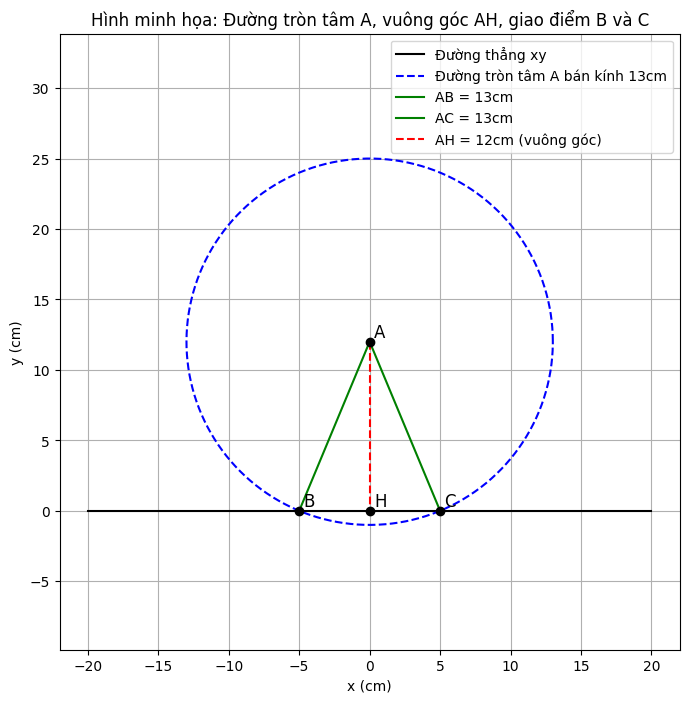
a) Chứng minh (A) có hai giao điểm với xy:
Vẽ AH vuông góc với xy tại H: Vì A cách đường thẳng xy là 12cm, nên AH = 12cm.
So sánh AH với bán kính R của đường tròn (A; 13cm):
Vẽ AH vuông góc với xy tại H: Vì A cách đường thẳng xy là 12cm, nên AH = 12cm.
So sánh AH với bán kính R của đường tròn (A; 13cm):
Ta có AH = 12cm và R = 13cm.
Vì AH < R (12cm < 13cm), nên đường thẳng xy cắt đường tròn (A; 13cm) tại hai điểm phân biệt.
Kết luận: Vậy đường tròn (A) có hai giao điểm với xy.
b) Tính BC:
Gọi B và C là hai giao điểm của (A) và xy: Theo đề bài.
Tính HB và HC: Vì AH vuông góc với BC tại H, nên H là trung điểm của BC (tính chất đường kính vuông góc với dây cung).
Kết luận: Vậy đường tròn (A) có hai giao điểm với xy.
b) Tính BC:
Gọi B và C là hai giao điểm của (A) và xy: Theo đề bài.
Tính HB và HC: Vì AH vuông góc với BC tại H, nên H là trung điểm của BC (tính chất đường kính vuông góc với dây cung).
Do đó, HB = HC. Áp dụng định lý Pitago cho tam giác AHB vuông tại H:
AB2 = AH2 + HB2
=>132 = 122 + HB2
=> 169 = 144 + HB2
=> HB2 = 25
=> HB = 5 (cm) Vậy, HB = HC = 5cm.
Tính BC: Vì H là trung điểm của BC, nên BC = 2 * HB = 2 * 5 = 10 (cm).
Kết luận:
a) Đường tròn (A) có hai giao điểm với xy.
Tính BC: Vì H là trung điểm của BC, nên BC = 2 * HB = 2 * 5 = 10 (cm).
Kết luận:
a) Đường tròn (A) có hai giao điểm với xy.
b) BC = 10cm.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
17097
Đã trả lời bởi chuyên gia
17097 -
 Đã trả lời bởi chuyên gia
8623
Đã trả lời bởi chuyên gia
8623 -
 Đã trả lời bởi chuyên gia
4946
Đã trả lời bởi chuyên gia
4946 -
 Đã trả lời bởi chuyên gia
4570
Đã trả lời bởi chuyên gia
4570 -
 Đã trả lời bởi chuyên gia
4130
Đã trả lời bởi chuyên gia
4130
Gửi báo cáo thành công!


