Cho tam giác ABC cân tại A có góc A = 36 độ . Phân giác BD và đường cao AH cắt nhau tại I . Tia phân giác góc ADB cắt AH tại O . Gọi E là giao điểm của BO và AC ; F là giao điểm của CI và DO . CMR các tứ giác BCEF và BDAF là các hình thoi
Quảng cáo
1 câu trả lời 515
Bài giải:
∆ABC cân tại A, ∠A = 36°
⇒ ∠B = ∠C = (180° – 36°) : 2 = 72°
Vì ∆ABC cân tại A ⇒ AH là đường cao đồng thời là trung tuyến
⇒ H là trung điểm BC
Gọi BD là phân giác ∠B
→ ∠ABD = ∠DBA = 36°
Gọi O là giao điểm của phân giác ∠ADB và AH
→ ∠ADO = ∠BDO = 27°
Xét ∆BDO và ∆ADO có:
- DO chung
- ∠BDO = ∠ADO
→ ⇒ BD = DA
Chứng minh tương tự AF = FB
⇒ Tứ giác BDAF có 4 cạnh bằng nhau ⇒ là hình thoi
Tứ giác BCEF:
- Do tam giác ABC cân tại A
- AH là trục đối xứng
→ B đối xứng C, E đối xứng với C, F đối xứng với B
⇒ BCEF có 4 cạnh bằng nhau ⇒ là hình thoi
Đáp số: BDAF và BCEF là hình thoi.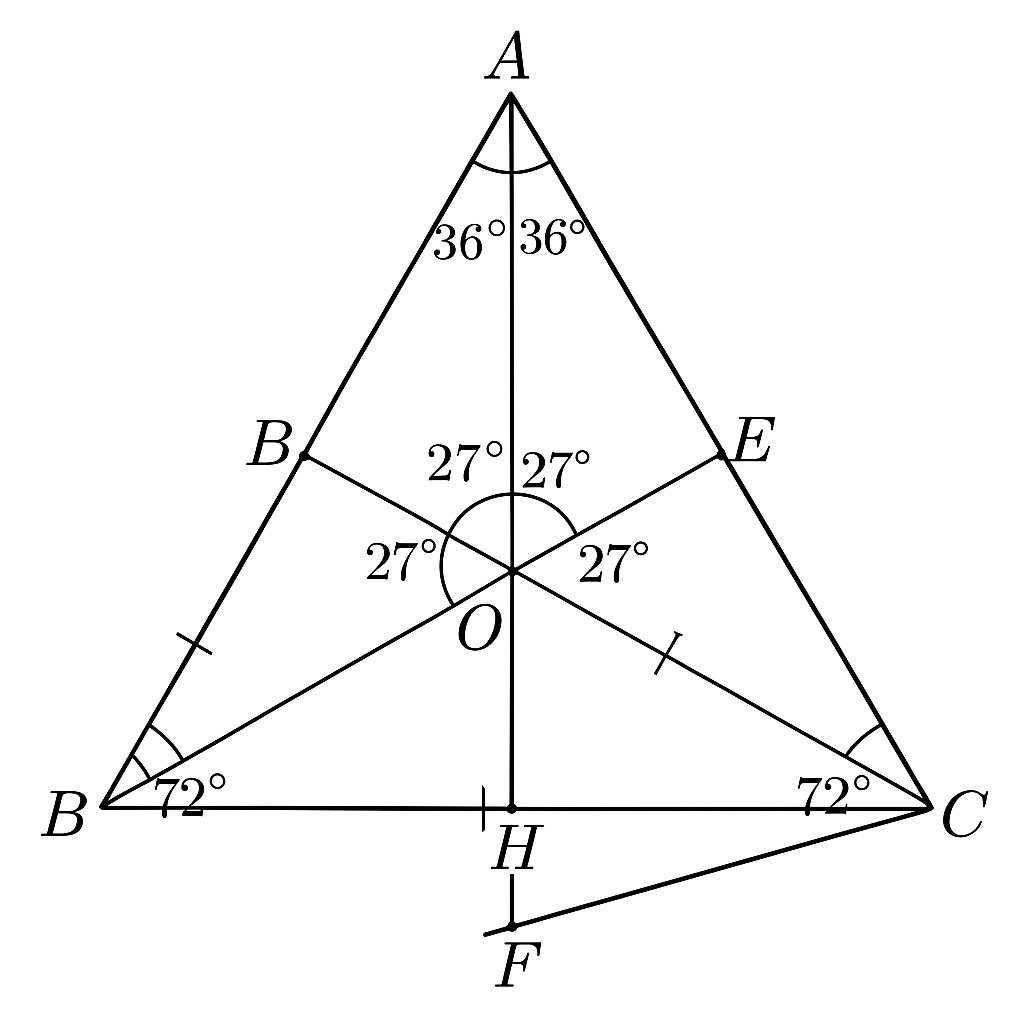
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
16070
-
8850


