a) Tìm giao tuyến của các cặp mặt phẳng (SAB) và (SCD), (SAC) và (SBD)
b) Tìm giao tuyến của (SEF) với các mặt phẳng (SAD), (SBC)
Quảng cáo
2 câu trả lời 3593
Giải thích các bước giải:
a.Ta có AB∩CD=E→E∈AB,E∈CDAB∩CD=E→E∈AB,E∈CD
→E∈(SAB),E∈(SCD)→E∈(SAB),E∈(SCD)
→(SAB)∩(SCD)=SE→(SAB)∩(SCD)=SE
Ta có AC∩BD=F→F∈AC,DB→F∈(SAC),(SBD)→(SAC)∩(SBD)=SFAC∩BD=F→F∈AC,DB→F∈(SAC),(SBD)→(SAC)∩(SBD)=SF
b.Gọi EF∩AD=GEF∩AD=G
→(SEF)∩(SAD)=SG→(SEF)∩(SAD)=SG
Gọi EF∩BC=H→(SEF)∩(SBC)=SH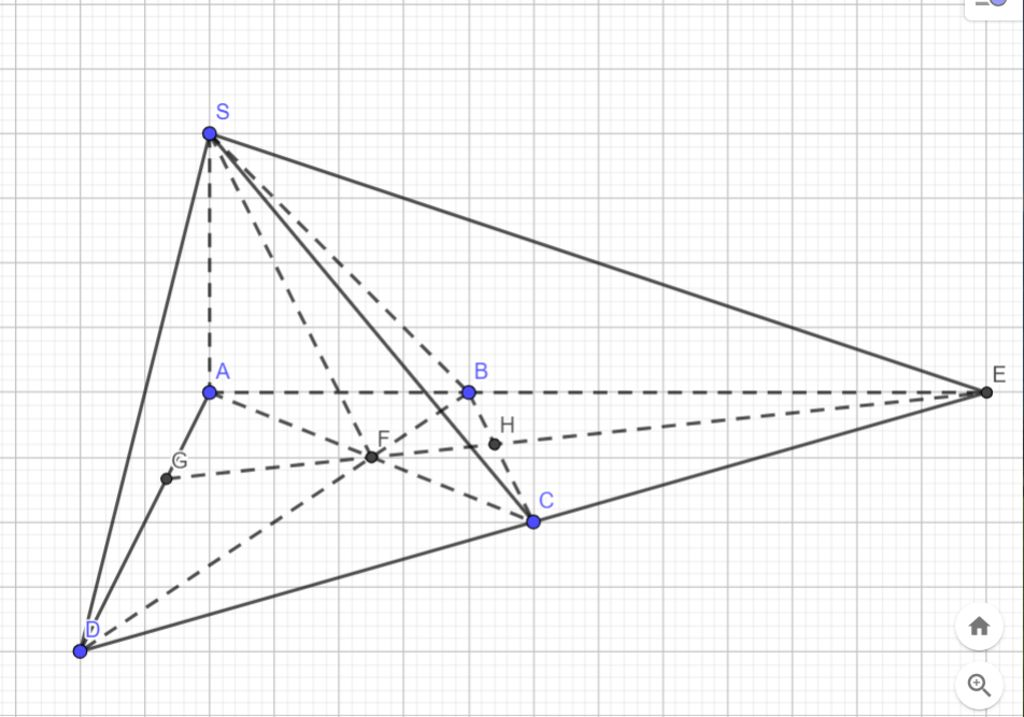
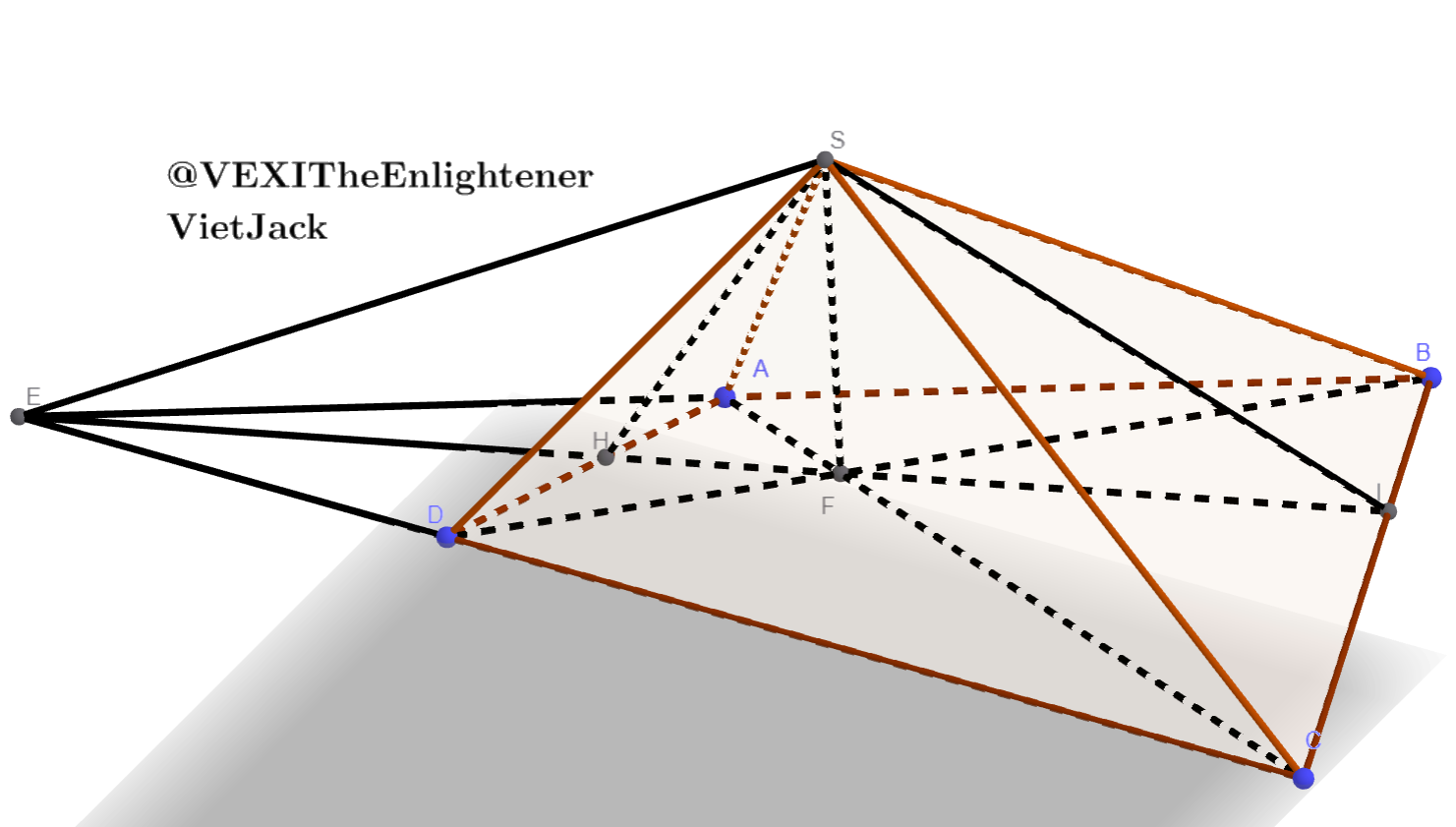
$\textbf{a}\bigg)$$\\$
Ta có: $AB \cap CD = E$$\\$
$\Rightarrow E \in (SAB) \cap (SCD)$$\\$
Mà $S \in (SAB) \cap (SCD)$$\\$
$\Rightarrow SE = (SAB) \cap (SCD)$$\\$
Ta có: $AC \cap BD = F$$\\$
$\Rightarrow F \in (SAC) \cap (SBD)$$\\$
Mà $S \in (SAC) \cap (SBD)$$\\$
$\Rightarrow SF = (SAC) \cap (SBD)$$\\$
$\textbf{b}\bigg)$$\\$
Trong $(SEF)$, gọi $H = EF \cap AD, I = EF \cap BC$
Ta có: $EF \cap AD = H$$\\$
$\Rightarrow H \in (SEF) \cap (SAD)$$\\$
Mà $S \in (SEF) \cap (SAD)$$\\$
$\Rightarrow SH = (SEF) \cap (SAD)$$\\$
Ta có: $EF \cap BC = I$$\\$
$\Rightarrow I \in (SEF) \cap (SBC)$$\\$
Mà $S \in (SEF) \cap (SBC)$$\\$
$\Rightarrow SI = (SEF) \cap (SBC)$
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
zytera
1325 điểm
-
Dương Nguyễn
960 điểm
-
보고 싶어요
855 điểm
-
돈이없다 💸😭
815 điểm
-
우옌 ✨
790 điểm
-
`d.`
635 điểm
-
`color{blue}text{HuyTùng.`
555 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
540 điểm
-
주디 홉스닉주디🥵👍
520 điểm
-
‧₊˚✩ ₊˚🎧⊹♡≽☁˚˖ִ໋🌷͙֒✧˚.🎀༘⋆⋅♡👾đẹρ-†®åî⋆⭒💫
435 điểm
-
Ngọc Linh hay nói linh tinh
385 điểm
-
Kiều Anh 350 điểm
-
누가 고철을 팔고 싶어할까요🗑️🗑️
345 điểm
-
Bích Hồng 345 điểm
Rút gọn
Bài viết mới nhất Lớp 11
-
3 năm trước3540
-
3 năm trước3381
