Cho tam giác ABC vuông tại A có AB <AC, đường cao AH. Trên tia HC lấy D sao cho HD=HB .kẻ CE vuông góc với AD tại E. Đường thẳng CE cắt đường thẳng AH tại F.chứng minh FD vuông góc với Ac.tính số đó góc ACB
Quảng cáo
2 câu trả lời 800
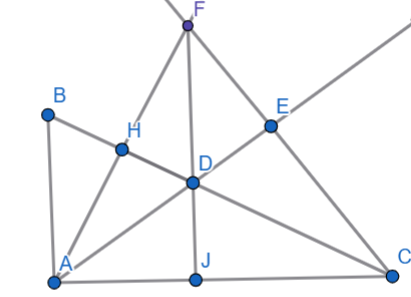
a. Xét tam giác AFC có CH và AE là 2 đường cao cắt nhau tại D
D là trực tâm của tam giác AFC
do đó
Phần a: Chứng minh FD⟂ACcap F cap D ⟂ cap A cap C
𝐹𝐷⟂𝐴𝐶
Bước 1: Chứng minh △AHB≅△AHDtriangle cap A cap H cap B is congruent to triangle cap A cap H cap D
△𝐴𝐻𝐵≅△𝐴𝐻𝐷
Ta có HB = HD (gt), \angle AHB = \angle AHD = 90^\circ, AH là cạnh chung, Vậy \triangle AHB \cong \triangle AHD (c.g.c).
Bước 2: Chứng minh ∠ACB=∠HACangle cap A cap C cap B equals angle cap H cap A cap C
∠𝐴𝐶𝐵=∠𝐻𝐴𝐶
Vì △AHB≅△AHDtriangle cap A cap H cap B is congruent to triangle cap A cap H cap D
△𝐴𝐻𝐵≅△𝐴𝐻𝐷
nên ∠HAB=∠HADangle cap H cap A cap B equals angle cap H cap A cap D
∠𝐻𝐴𝐵=∠𝐻𝐴𝐷
.
Trong tam giác ABCcap A cap B cap C
𝐴𝐵𝐶
, ta có ∠HAB+∠ACB=90∘angle cap H cap A cap B plus angle cap A cap C cap B equals 90 raised to the exponent composed with end-exponent
∠𝐻𝐴𝐵+∠𝐴𝐶𝐵=90∘
.
Vì ∠HAD=∠HABangle cap H cap A cap D equals angle cap H cap A cap B
∠𝐻𝐴𝐷=∠𝐻𝐴𝐵
, ta có ∠ACB=∠HACangle cap A cap C cap B equals angle cap H cap A cap C
∠𝐴𝐶𝐵=∠𝐻𝐴𝐶
.
Bước 3: Chứng minh ∠AFD=90∘angle cap A cap F cap D equals 90 raised to the exponent composed with end-exponent
∠𝐴𝐹𝐷=90∘
Ta có ∠AFE=90∘angle cap A cap F cap E equals 90 raised to the exponent composed with end-exponent
∠𝐴𝐹𝐸=90∘
(vì CE⟂ADcap C cap E ⟂ cap A cap D
𝐶𝐸⟂𝐴𝐷
tại Ecap E
𝐸
).
∠AFD=90∘−∠CAF=90∘−∠ACBangle cap A cap F cap D equals 90 raised to the exponent composed with end-exponent minus angle cap C cap A cap F equals 90 raised to the exponent composed with end-exponent minus angle cap A cap C cap B
∠𝐴𝐹𝐷=90∘−∠𝐶𝐴𝐹=90∘−∠𝐴𝐶𝐵
.
Mà ∠ACB=∠HACangle cap A cap C cap B equals angle cap H cap A cap C
∠𝐴𝐶𝐵=∠𝐻𝐴𝐶
, nên ∠AFD=90∘−∠HACangle cap A cap F cap D equals 90 raised to the exponent composed with end-exponent minus angle cap H cap A cap C
∠𝐴𝐹𝐷=90∘−∠𝐻𝐴𝐶
.
Trong tam giác AFCcap A cap F cap C
𝐴𝐹𝐶
, ta có ∠AFC+∠CAF+∠ACF=180∘angle cap A cap F cap C plus angle cap C cap A cap F plus angle cap A cap C cap F equals 180 raised to the exponent composed with end-exponent
∠𝐴𝐹𝐶+∠𝐶𝐴𝐹+∠𝐴𝐶𝐹=180∘
.
∠AFC=180∘−∠CAF−∠ACF=180∘−∠HAC−∠ACFangle cap A cap F cap C equals 180 raised to the exponent composed with end-exponent minus angle cap C cap A cap F minus angle cap A cap C cap F equals 180 raised to the exponent composed with end-exponent minus angle cap H cap A cap C minus angle cap A cap C cap F
∠𝐴𝐹𝐶=180∘−∠𝐶𝐴𝐹−∠𝐴𝐶𝐹=180∘−∠𝐻𝐴𝐶−∠𝐴𝐶𝐹
.
∠AFD=90∘angle cap A cap F cap D equals 90 raised to the exponent composed with end-exponent
∠𝐴𝐹𝐷=90∘
, nên FD⟂ACcap F cap D ⟂ cap A cap C
𝐹𝐷⟂𝐴𝐶
.
Phần b: Tính số đo góc ACB Ta có AH \perp BC, \angle ACB = \angle HAC, \angle HAB + \angle HAC = 90^\circ, \angle ACB = \angle HAC = 30^\circ.
Vậy ∠ACB=30∘angle cap A cap C cap B equals 30 raised to the exponent composed with end-exponent
∠𝐴𝐶𝐵=30∘
.
𝐹𝐷⟂𝐴𝐶
Bước 1: Chứng minh △AHB≅△AHDtriangle cap A cap H cap B is congruent to triangle cap A cap H cap D
△𝐴𝐻𝐵≅△𝐴𝐻𝐷
Ta có HB = HD (gt), \angle AHB = \angle AHD = 90^\circ, AH là cạnh chung, Vậy \triangle AHB \cong \triangle AHD (c.g.c).
Bước 2: Chứng minh ∠ACB=∠HACangle cap A cap C cap B equals angle cap H cap A cap C
∠𝐴𝐶𝐵=∠𝐻𝐴𝐶
Vì △AHB≅△AHDtriangle cap A cap H cap B is congruent to triangle cap A cap H cap D
△𝐴𝐻𝐵≅△𝐴𝐻𝐷
nên ∠HAB=∠HADangle cap H cap A cap B equals angle cap H cap A cap D
∠𝐻𝐴𝐵=∠𝐻𝐴𝐷
.
Trong tam giác ABCcap A cap B cap C
𝐴𝐵𝐶
, ta có ∠HAB+∠ACB=90∘angle cap H cap A cap B plus angle cap A cap C cap B equals 90 raised to the exponent composed with end-exponent
∠𝐻𝐴𝐵+∠𝐴𝐶𝐵=90∘
.
Vì ∠HAD=∠HABangle cap H cap A cap D equals angle cap H cap A cap B
∠𝐻𝐴𝐷=∠𝐻𝐴𝐵
, ta có ∠ACB=∠HACangle cap A cap C cap B equals angle cap H cap A cap C
∠𝐴𝐶𝐵=∠𝐻𝐴𝐶
.
Bước 3: Chứng minh ∠AFD=90∘angle cap A cap F cap D equals 90 raised to the exponent composed with end-exponent
∠𝐴𝐹𝐷=90∘
Ta có ∠AFE=90∘angle cap A cap F cap E equals 90 raised to the exponent composed with end-exponent
∠𝐴𝐹𝐸=90∘
(vì CE⟂ADcap C cap E ⟂ cap A cap D
𝐶𝐸⟂𝐴𝐷
tại Ecap E
𝐸
).
∠AFD=90∘−∠CAF=90∘−∠ACBangle cap A cap F cap D equals 90 raised to the exponent composed with end-exponent minus angle cap C cap A cap F equals 90 raised to the exponent composed with end-exponent minus angle cap A cap C cap B
∠𝐴𝐹𝐷=90∘−∠𝐶𝐴𝐹=90∘−∠𝐴𝐶𝐵
.
Mà ∠ACB=∠HACangle cap A cap C cap B equals angle cap H cap A cap C
∠𝐴𝐶𝐵=∠𝐻𝐴𝐶
, nên ∠AFD=90∘−∠HACangle cap A cap F cap D equals 90 raised to the exponent composed with end-exponent minus angle cap H cap A cap C
∠𝐴𝐹𝐷=90∘−∠𝐻𝐴𝐶
.
Trong tam giác AFCcap A cap F cap C
𝐴𝐹𝐶
, ta có ∠AFC+∠CAF+∠ACF=180∘angle cap A cap F cap C plus angle cap C cap A cap F plus angle cap A cap C cap F equals 180 raised to the exponent composed with end-exponent
∠𝐴𝐹𝐶+∠𝐶𝐴𝐹+∠𝐴𝐶𝐹=180∘
.
∠AFC=180∘−∠CAF−∠ACF=180∘−∠HAC−∠ACFangle cap A cap F cap C equals 180 raised to the exponent composed with end-exponent minus angle cap C cap A cap F minus angle cap A cap C cap F equals 180 raised to the exponent composed with end-exponent minus angle cap H cap A cap C minus angle cap A cap C cap F
∠𝐴𝐹𝐶=180∘−∠𝐶𝐴𝐹−∠𝐴𝐶𝐹=180∘−∠𝐻𝐴𝐶−∠𝐴𝐶𝐹
.
∠AFD=90∘angle cap A cap F cap D equals 90 raised to the exponent composed with end-exponent
∠𝐴𝐹𝐷=90∘
, nên FD⟂ACcap F cap D ⟂ cap A cap C
𝐹𝐷⟂𝐴𝐶
.
Phần b: Tính số đo góc ACB Ta có AH \perp BC, \angle ACB = \angle HAC, \angle HAB + \angle HAC = 90^\circ, \angle ACB = \angle HAC = 30^\circ.
Vậy ∠ACB=30∘angle cap A cap C cap B equals 30 raised to the exponent composed with end-exponent
∠𝐴𝐶𝐵=30∘
.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669
Gửi báo cáo thành công!


