cho tam giác ABC cân tại A . Trung tuyến AM. a, Chứng minh AM vuông góc với BC . b, Gọi E là trung điểm của AC . Trên tia đối của tia ME lấy D sao cho MD bằng ME .Chứng minh DC vuông góc với BC và AD // BC
Quảng cáo
2 câu trả lời 150
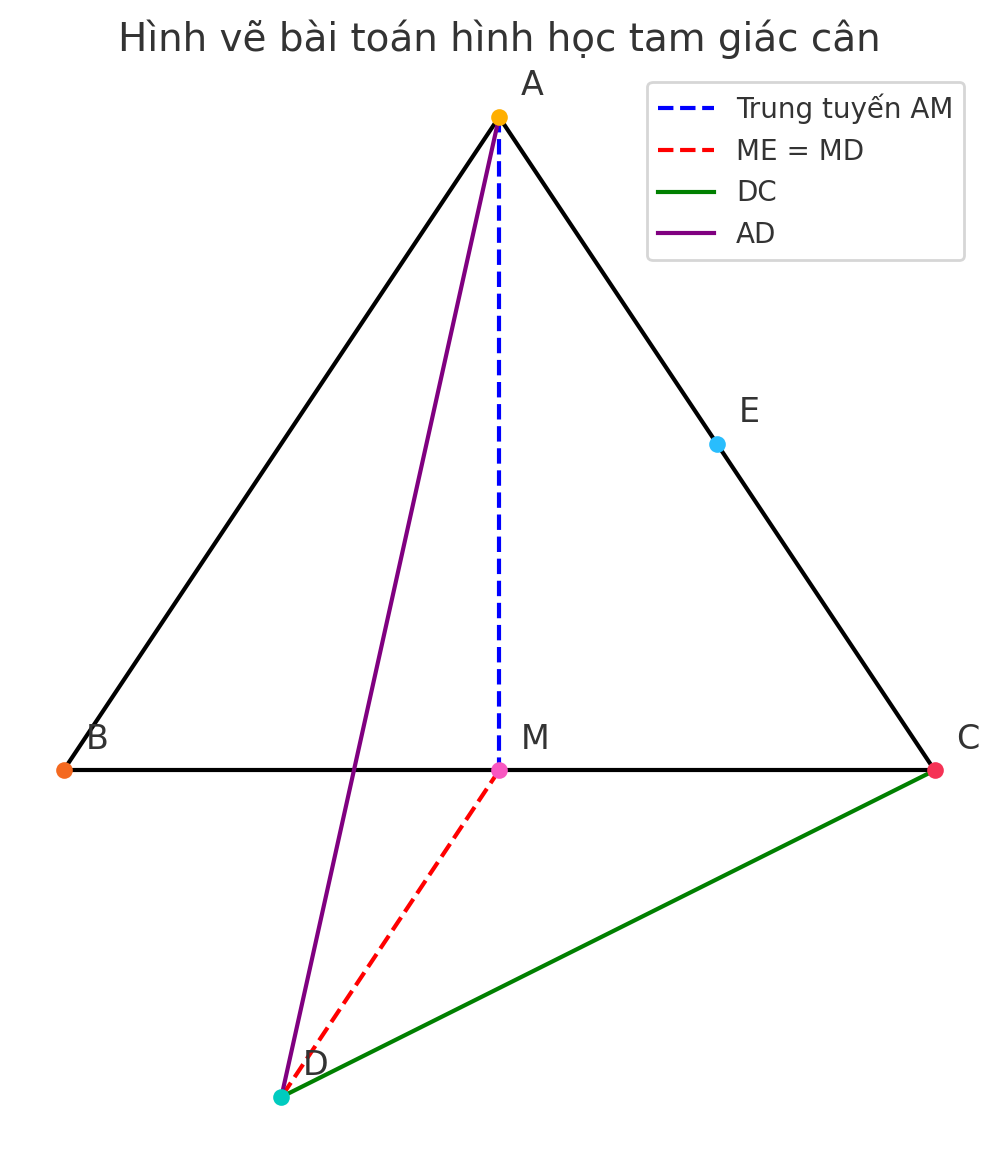
a) Vì AB=AC (gt), nên tam giác △ABC cân tại A ⇒ trung tuyến AM đồng thời là đường cao.
⇒AM⊥BC
b) Gọi EEE là trung điểm của AC
⇒ AE=EC, mà M là trung điểm BC, xét đoạn ME
Lấy điểm D trên tia đối của tia ME sao cho:
Vì △ABC cân tại A, nên AM⊥BC, mà D,E đối xứng nhau qua M, nên:
DC⊥BC
- AM⊥BC
-
DC⊥BC
-
AD∥BC
a, Chứng minh AM vuông góc với BC
Xét △ABM và △ACM:
AB=AC (vì △ABC cân tại A).
BM=CM (vì M là trung điểm của BC).
AM là cạnh chung.
Do đó, △ABM≅△ACM (theo trường hợp cạnh-cạnh-cạnh - SSS).
Từ tính chất hai tam giác bằng nhau, suy ra các góc tương ứng bằng nhau: ∠AMB=∠AMC.
Mà ∠AMB và ∠AMC là hai góc kề bù (tổng bằng 180∘).
Vậy ∠AMB=∠AMC=2180∘=90∘.
Điều này có nghĩa là AM⊥BC.
Kết luận: AM vuông góc với BC.
b, Gọi E là trung điểm của AC. Trên tia đối của tia ME lấy D sao cho MD bằng ME. Chứng minh DC vuông góc với BC và AD // BC.
Phần này của đề bài có vẻ không đúng với mọi tam giác ABC cân tại A. Chúng ta sẽ phân tích các tính chất hình học từ việc dựng điểm D và sau đó kiểm tra lại các yêu cầu chứng minh.
Bước 1: Chứng minh BDEC là hình bình hành.
Ta có M là trung điểm của BC (theo giả thiết).
Ta có M là trung điểm của DE (vì D nằm trên tia đối của ME và MD=ME).
Một tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Vậy, tứ giác BDEC là hình bình hành.
Từ đó, ta suy ra các cặp cạnh đối song song: DC∥BE và BD∥CE.
Bước 2: Chứng minh ABED là hình bình hành.
Xét △ABC: M là trung điểm của BC, E là trung điểm của AC.
Do đó, ME là đường trung bình của △ABC.
Từ tính chất đường trung bình, ta có ME∥AB và ME=21AB.
Vì D nằm trên tia đối của ME và MD=ME, nên DE nằm trên đường thẳng chứa ME.
Suy ra DE∥AB.
Đồng thời, DE=MD+ME=ME+ME=2ME.
Mà ME=21AB, nên DE=2⋅21AB=AB.
Một tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành.
Vậy, tứ giác ABED là hình bình hành.
Từ đó, ta suy ra AD∥BE và AD=BE.
Bước 3: Kiểm tra các yêu cầu chứng minh.
Yêu cầu 1: Chứng minh DC⊥BC.
Từ Bước 1, ta có DC∥BE.
Để DC⊥BC, thì BE cũng phải vuông góc với BC.
Tức là △BME phải vuông tại M.
Điều này chỉ xảy ra khi BE thẳng hàng với AM (vì AM⊥BC).
Tuy nhiên, BE không nhất thiết phải song song với AM trong mọi trường hợp tam giác ABC cân tại A.
Ví dụ, nếu A=(0,a), B=(−b,0), C=(b,0), thì M=(0,0). E=(2b,2a). D=(−2b,−2a).
BC =(2b,0). DC =(b−(−2b),0−(−2a))=(23b,2a).
Tích vô hướng DC ⋅BC =(23b)(2b)+(2a)(0)=3b2.
Để tích vô hướng bằng 0 (tức là vuông góc), thì 3b2=0⟹b=0. Điều này có nghĩa là B,C,M trùng nhau, không tạo thành tam giác.
Do đó, DC⊥BC không đúng với mọi tam giác ABC cân tại A.
Yêu cầu 2: Chứng minh AD∥BC.
Từ Bước 2, ta có AD∥BE.
Từ Bước 1, ta có DC∥BE.
Điều này có nghĩa là AD∥DC.
Nếu AD∥DC, thì A,D,C phải thẳng hàng.
Tuy nhiên, A,D,C không thẳng hàng trong một tam giác thông thường.
Ví dụ, từ tọa độ đã dùng ở trên: A=(0,a), D=(−2b,−2a), C=(b,0).
AD =(−2b,−23a). AC =(b,−a).
Để A,D,C thẳng hàng, AD phải là bội của AC .
(−2b,−23a)=k(b,−a).
−2b=kb và −23a=−ka.
Từ −2b=kb, nếu b=0, thì k=−21.
Thay k=−21 vào −23a=−ka, ta có −23a=−(−21)a=21a.
Điều này chỉ đúng khi a=0, tức là A nằm trên BC, không tạo thành tam giác.
Do đó, AD∥BC cũng không đúng với mọi tam giác ABC cân tại A.
Kết luận chung cho phần b):
Có vẻ như có một lỗi trong đề bài ở phần b). Với các dữ kiện đã cho và cách dựng hình, không thể chứng minh được DC⊥BC và AD∥BC cho mọi tam giác ABC cân tại A.
Tuy nhiên, từ việc dựng hình, chúng ta có thể chứng minh được một số tính chất khác:
BDEC là hình bình hành.
ABED là hình bình hành.
BD∥AC (vì BD∥CE và E nằm trên AC).
DC∥AB (vì DC∥BE và BE∥AD, nên DC∥AD. Lại có AD∥BE, BE∥DC. Mà AB∥DE, nên AB∥DC).
Nếu đề bài có ý muốn hỏi những tính chất này thì có thể chứng minh được.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669


