Bài 3: Cho tg ABC có ba góc nhọn, trung tuyến AM, trên nửa mặt phẳng chứa điểm C bờ là đường thẳng AB, vẽ AE vuông góc với AB và AE=AB, trên nửa mặt phẳng bờ AC chứa điểm B vẽ AD vuông góc với AC và AD=AC
a, CMR: BD=CE
b, Trên tia đối của tia MA lấy điểm N sao cho MN=MA,
CMR : tg ADE= tg CAN
c, Gọi I là giao của DE và AM, CMR:(AD^2+IE^2)/(DI^2+AE^2)=1
Quảng cáo
2 câu trả lời 177
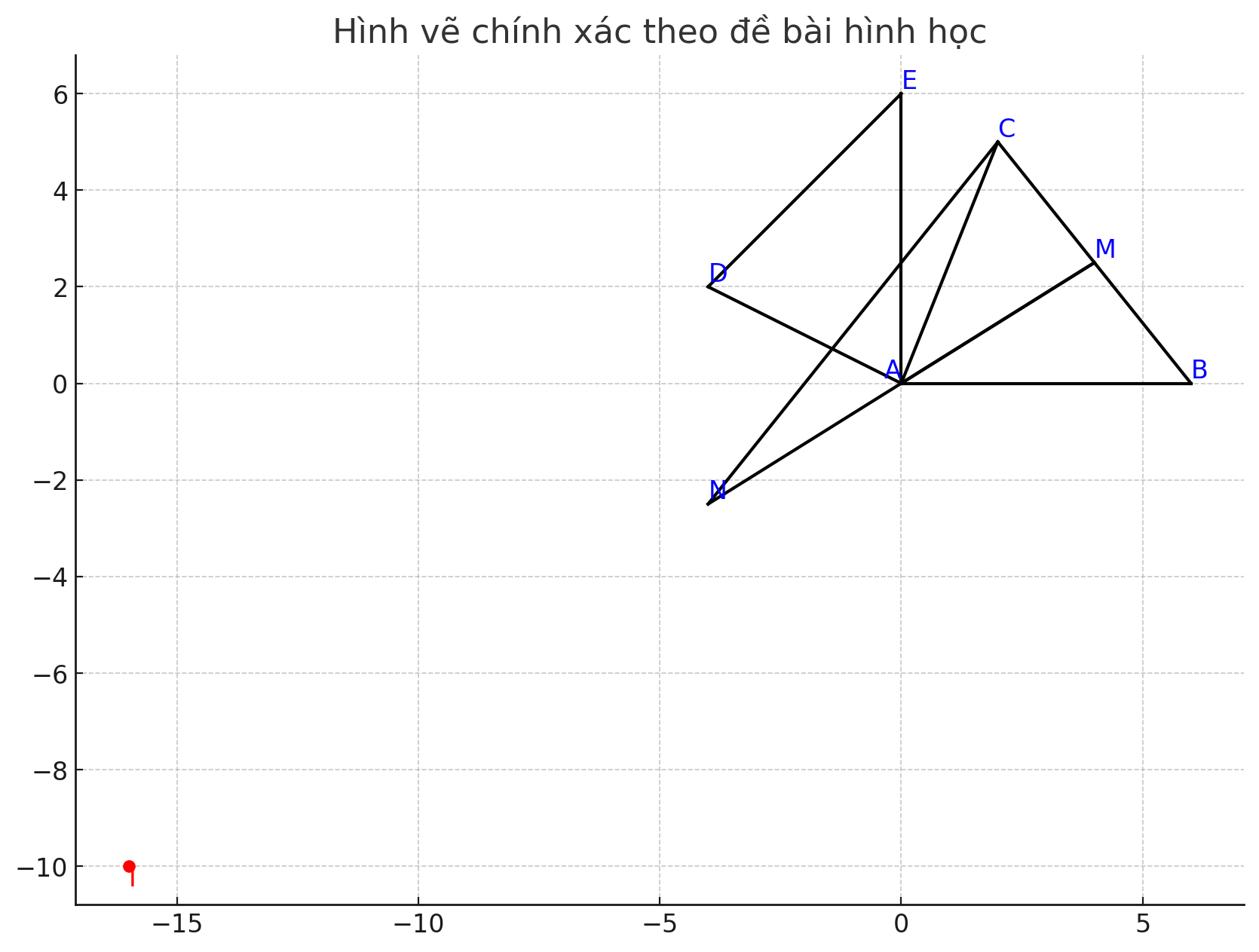
Xét tam giác ABD và ACE:
- AD⊥AC, AD=AC ⇒ tam giác ACD vuông cân tại D.
- AE⊥AB, AE=AB ⇒ tam giác ABE vuông cân tại E.
→ Hai tam giác ACD và ABE có cùng độ dài hai cạnh kề vuông và góc vuông.
Ta quay tam giác ACD một góc 90 quanh điểm A để đưa về tam giác ABE. Khi đó:
- AC↦AB
- D↦E
→ CD↦BE
Mà M là trung điểm của BC, nên nếu ta quay đoạn CD sang BE, ta sẽ có:
- AE=AB, AD=AC (dữ kiện đề)
- AB=AE, AC=AD ⇒ AE=AC, AD=AB (do các cặp bằng nhau)
- Tam giác ADE: góc ∠DAE=90+90=180−∠A (Tổng góc vuông tại D và E)
→ Ta sử dụng phép đối xứng trục qua đường thẳng AM, kết hợp tịnh tiến để đưa tam giác ADE sang CAN
- MA=MN, đối xứng qua điểm A, giữ nguyên chiều dài
- Cạnh tương ứng bằng nhau: AD=AC, AE=AB
- Góc xen giữa tương ứng
=Suy ra: △ADE≅△CAN (c.g.c )
Ta có:
Trong tam giác vuông ADI, cạnh huyền là AD, các cạnh góc vuông là DI và AI:
Ta có:
`AD = AC` (giả thiết)
`AE = AB` (giả thiết)
`∠DAE = ∠BAC` (cùng phụ với `∠BAE` và `∠DAC`)
Do đó, `ΔDAE = ΔBAC`(c.g.c)
Từ đó, ta có:
`BD = CE` (hai cạnh tương ứng)
`b)`
Ta có:
`MN = MA` (giả thiết)
`∠AMN = ∠AMC` (đối đỉnh)
Do đó, `ΔAMN ≅ ΔAMC (c.g.c)`
Từ đó, ta có:
`AN = AC` (hai cạnh tương ứng)
`∠NAC = ∠MAC` (hai góc tương ứng)
Ta lại có:
`AD = AC` (giả thiết)
`AE = AB` (giả thiết)
Do đó, `ΔADE = ΔCAN (c.g.c)`
`c)` chx lm
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669


