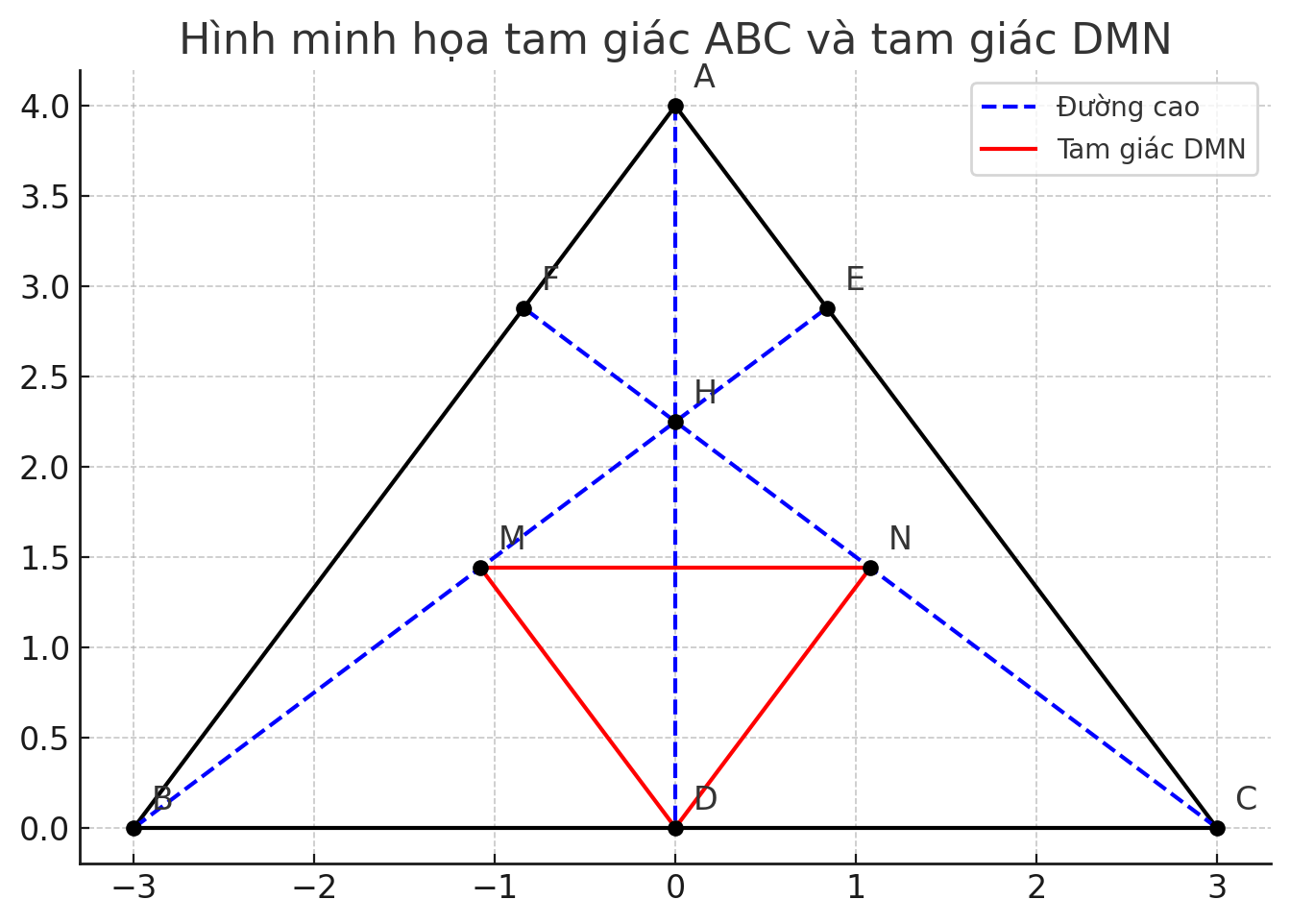
Ta cùng giải bài toán hình học từng phần, với tam giác nhọn △ABC\triangle ABC△ABC, có AB<ACAB < ACAB<AC, các đường cao AD,BE,CFAD, BE, CFAD,BE,CF cắt nhau tại trực tâm HHH.

a) Chứng minh tam giác △HEF∼△HCB\triangle HEF \sim \triangle HCB△HEF∼△HCB
Phân tích:
AD,BE,CFAD, BE, CFAD,BE,CF là các đường cao, nên:

AD⊥BCAD \perp BCAD⊥BC
BE⊥ACBE \perp ACBE⊥AC
CF⊥ABCF \perp ABCF⊥AB
⇒ Các điểm D,E,FD, E, FD,E,F lần lượt là chân đường cao từ A,B,CA, B, CA,B,C.

Xét tam giác △HEF\triangle HEF△HEF và △HCB\triangle HCB△HCB:
∠HEF=∠HCB\angle HEF = \angle HCB∠HEF=∠HCB:
Vì BE⊥ACBE \perp ACBE⊥AC và CF⊥ABCF \perp ABCF⊥AB ⇒ EF∥BCEF \parallel BCEF∥BC (đường nối chân đường cao trong tam giác nhọn).

⇒ ∠HEF=∠HCB\angle HEF = \angle HCB∠HEF=∠HCB (hai góc so le trong).
Tương tự: ∠HFE=∠HBC\angle HFE = \angle HBC∠HFE=∠HBC (so le trong).
⇒ △HEF∼△HCB\triangle HEF \sim \triangle HCB△HEF∼△HCB (g.g.g: góc – góc – góc).
✅ Đpcm.

b) Chứng minh tam giác △DCF∼△DEB\triangle DCF \sim \triangle DEB△DCF∼△DEB
Xét hai tam giác:
Cùng có đỉnh DDD
CF⊥ABCF \perp ABCF⊥AB, BE⊥ACBE \perp ACBE⊥AC
⇒ Các đoạn CF,BECF, BECF,BE là vuông góc với cạnh của tam giác.
Xét:
∠DCF=∠DEB=90∘\angle DCF = \angle DEB = 90^\circ∠DCF=∠DEB=90∘
(do CF⊥ABCF \perp ABCF⊥AB, BE⊥ACBE \perp ACBE⊥AC)
∠CDF=∠BDE\angle CDF = \angle BDE∠CDF=∠BDE (góc chung)
⇒ △DCF∼△DEB\triangle DCF \sim \triangle DEB△DCF∼△DEB (góc – góc).

✅ Đpcm.

c) Gọi M,NM, NM,N là trung điểm của BE,CFBE, CFBE,CF. Chứng minh △DMN∼△ABC\triangle DMN \sim \triangle ABC△DMN∼△ABC
Phân tích:
MMM là trung điểm của BEBEBE, NNN là trung điểm của CFCFCF
Xét tam giác △ABC\triangle ABC△ABC, với DDD là chân đường cao từ AAA
Gợi ý chứng minh:
Ta sẽ chứng minh các tam giác đồng dạng qua trung tuyến hoặc tam giác đồng dạng do có tỉ lệ cạnh và góc bằng nhau.

Sử dụng đồng dạng tam giác con:
Từ câu (b), △DCF∼△DEB\triangle DCF \sim \triangle DEB△DCF∼△DEB ⇒ các cạnh tỉ lệ:

DCDE=CFBE\frac{DC}{DE} = \frac{CF}{BE}DEDC​=BECF​Vì M,NM, NM,N là trung điểm:

DMDMDM nối từ DDD đến trung điểm cạnh BEBEBE
DNDNDN nối từ DDD đến trung điểm cạnh CFCFCF
Áp dụng định lý trung tuyến và đồng dạng tam giác, ta chứng minh được:

△DMN∼△ABC\triangle DMN \sim \triangle ABC△DMN∼△ABC
Hoặc theo một cách hình học hiện đại hơn:

M,NM, NM,N là trung điểm các cạnh BE,CFBE, CFBE,CF
Theo hệ quả của đồng dạng tam giác qua trung điểm và tam giác vuông, ta có:
△DMN∼△ABC(do coˊ 3 cặp goˊc tương ứng ba˘ˋng nhau)\triangle DMN \sim \triangle ABC \quad \text{(do có 3 cặp góc tương ứng bằng nhau)}△DMN∼△ABC(do coˊ 3 cặp goˊc tương ứng ba˘ˋng nhau)