VẼ HÌNH VÀ LÀM Ạ
Cho ΔABC vuông tại A, kẻ phân giác BD của góc B (D thuộc AC).kẻ AH ⊥ BD, (H thuộc BD), AH cắt BC tại E.
a) Chứng minh: ΔBHA = ΔBHE.
b) Chứng minh: ED ⊥ BC .
c) Chứng minh: AD < DC.
d) Kẻ AK ⊥ BC (K thuộc BC). Chứng minh: AE là phân giác của góc CAK
Quảng cáo
1 câu trả lời 201
7 tháng trước
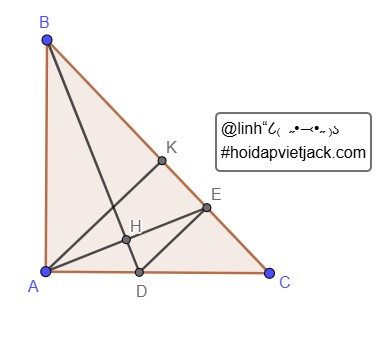
a)
Xét ΔBHA và ΔBHE có:
BH chung
∠BHA = ∠BHE = 90° (do AH ⊥ BD)
∠ABH = ∠EBH (do BD là phân giác của ∠B)
`=>` ΔBHA = ΔBHE (g.c.g)
b)
Từ ΔBHA = ΔBHE, suy ra BA = BE.
Xét ΔABD và ΔEBD có:
BD chung
∠ABD = ∠EBD (do BD là phân giác của ∠B)
BA = BE
`=>` ΔABD = ΔEBD (c.g.c)
`=>` ∠BAD = ∠BED = `90^@` (do ΔABC vuông tại A)
`=>` ED ⊥ BC.
c)
Từ ΔABD = ΔEBD `=>` AD = ED.
Xét ΔEDC vuông tại E, ta có:
DC > ED (cạnh huyền > cạnh góc vuông)
`=>` DC > AD hay AD < DC.
d)
Ta có ∠BAE = ∠BEA (do BA = BE)
Và ∠BAE + ∠EAK = 90°
∠BEA + ∠EAC = 90°
`=>` ∠EAK = ∠EAC
`=>` AE là phân giác của góc CAK.
Xét ΔBHA và ΔBHE có:
BH chung
∠BHA = ∠BHE = 90° (do AH ⊥ BD)
∠ABH = ∠EBH (do BD là phân giác của ∠B)
`=>` ΔBHA = ΔBHE (g.c.g)
b)
Từ ΔBHA = ΔBHE, suy ra BA = BE.
Xét ΔABD và ΔEBD có:
BD chung
∠ABD = ∠EBD (do BD là phân giác của ∠B)
BA = BE
`=>` ΔABD = ΔEBD (c.g.c)
`=>` ∠BAD = ∠BED = `90^@` (do ΔABC vuông tại A)
`=>` ED ⊥ BC.
c)
Từ ΔABD = ΔEBD `=>` AD = ED.
Xét ΔEDC vuông tại E, ta có:
DC > ED (cạnh huyền > cạnh góc vuông)
`=>` DC > AD hay AD < DC.
d)
Ta có ∠BAE = ∠BEA (do BA = BE)
Và ∠BAE + ∠EAK = 90°
∠BEA + ∠EAC = 90°
`=>` ∠EAK = ∠EAC
`=>` AE là phân giác của góc CAK.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120578
-
81263
-
59365
Gửi báo cáo thành công!


