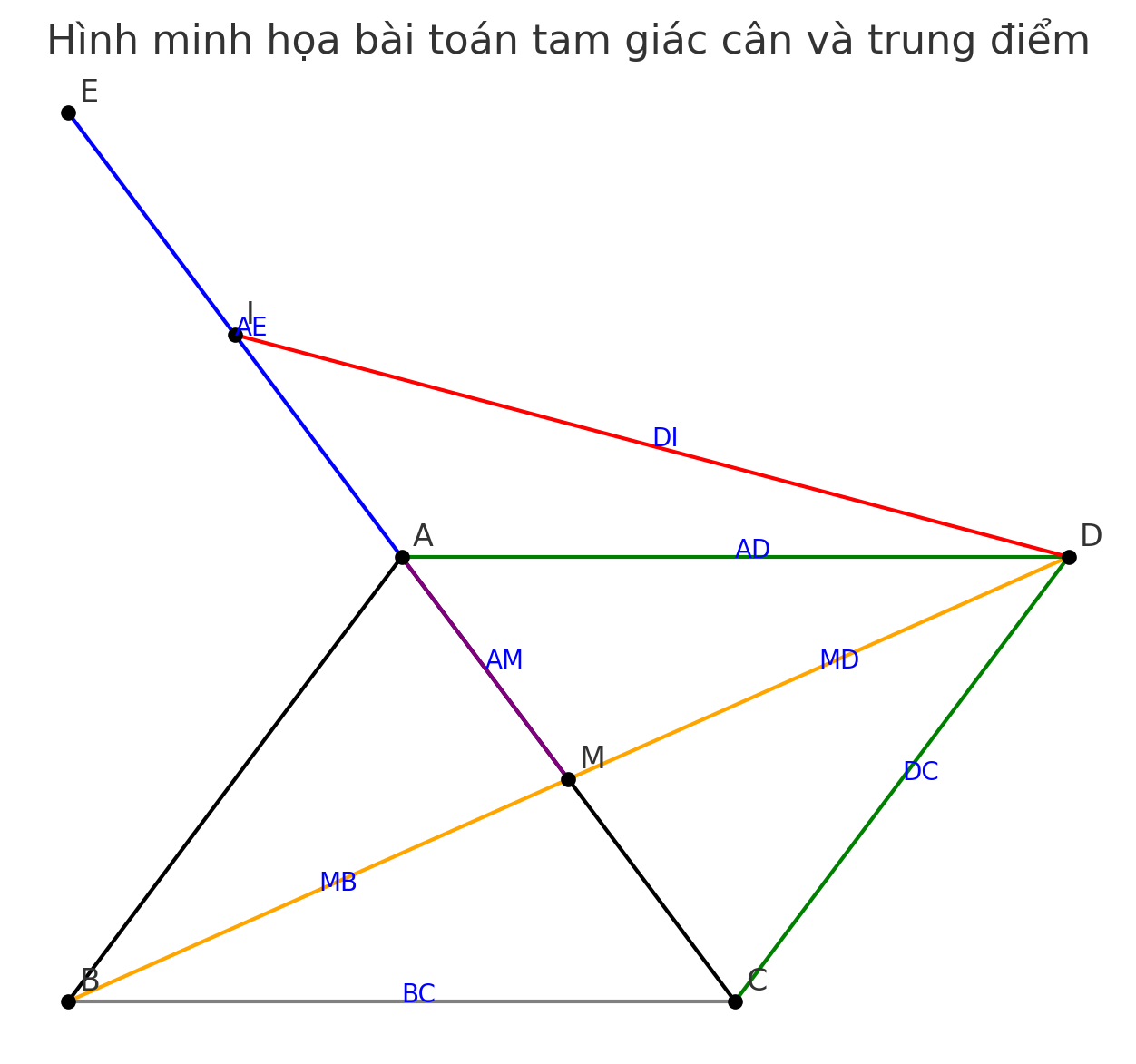
Cho tgiac ABC cân tại A. gọi M là trung điểm AC . trên tia đối của tia MB lấy điểm D sao cho DM=BM
a,chứng minh tgiac BMC= tgiac DMA . Suy ra AD//BC
b,Chúng minh tgiac ACD là tgiac cân
c, Trên tia đối của tia CA lấy điểm E sao cho CA=CE .Chứng minh DC đi qua trung điểm I
Quảng cáo
2 câu trả lời 201
a) Chứng minh ΔBMC = ΔDMA. Suy ra AD // BC
Chứng minh ΔBMC = ΔDMA:
- M là trung điểm AC ⇒ AM = MC
- Cho DM = BM (theo giả thiết)
- Hai tam giác BMC và DMA có:
- \( BM = DM \) (GT)
- \( MC = AM \) (do M là trung điểm AC)
- \( \angle BMC = \angle DMA \) (đối đỉnh)
⇒ ΔBMC = ΔDMA (c.g.c)
Suy ra: AD // BC
- ΔBMC = ΔDMA ⇒ góc BMC = góc DMA
- Mà hai góc này nằm ở vị trí so le trong
- ⇒ AD // BC (vì hai góc so le trong bằng nhau)
ΔBMC = ΔDMA, suy ra AD // BC
b) Chứng minh ΔACD là tam giác cân
Ta đã biết:
- M là trung điểm của AC ⇒ AM = MC
- DM = BM (GT)
- ΔBMC = ΔDMA ⇒ từ đó có: MC = AD
Mà AC là cạnh chung ⇒
\[
AD = MC = AM = \frac{AC}{2}
\Rightarrow AD = DC
\]
→ Trong tam giác ACD có AD = DC ⇒ tam giác ACD cân tại D
ΔACD là tam giác cân tại D
c) Trên tia đối của CA lấy điểm E sao cho CA = CE. Chứng minh DC đi qua trung điểm I của AE
- Vì CA = CE, mà E nằm trên tia đối của CA ⇒ A là trung điểm của đoạn CE
- Gọi I là trung điểm đoạn AE
→ Ta cần chứng minh đường thẳng DC đi qua I
- Tam giác ACD cân tại D (đã chứng minh ở trên)
- Gọi O là trung điểm AC
- E đối xứng với C qua A ⇒ đoạn CE đối xứng qua A
⇒ A là trung điểm CE ⇒ AE = EC, mà AC = AE (đối xứng)
⇒ Tam giác ACE cân tại A
- Do D đối xứng B qua M (từ phần a), và A là trung điểm CE ⇒ D và C đối xứng qua trung điểm I của AE
→ Suy ra: DC đi qua trung điểm I của AE
Đường thẳng DC đi qua trung điểm I của AE
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
12423
-
 Đã trả lời bởi chuyên gia
5747
Đã trả lời bởi chuyên gia
5747 -
4835


