Một hình thang có độ dài hai đáy lần lượt là 12 cm và 8 cm, chiều cao là 6 cm.
Người ta kẻ thêm một đường thẳng song song với hai đáy, chia hình thang thành hai hình thang nhỏ có diện tích bằng nhau.
Hỏi đường thẳng đó cách đáy lớn bao nhiêu cm?
Quảng cáo
3 câu trả lời 244
Gọi đáy của phần trên đường chia là \( a_1 = 12 \), đáy dưới là \( a_2 = 8 \)
Gọi độ dài đáy mới chia hình thang thành hai phần là \( d \) (cm)
⇒ Khi đó:
- Hình thang trên: đáy trên 12 cm, đáy dưới \( d \), chiều cao = x
- Hình thang dưới: đáy trên \( d \), đáy dưới 8 cm, chiều cao = 6 – x
Tính diện tích hình thang lớn
\[
S = \frac{(12 + 8)}{2} \cdot 6 = 60 \, \text{cm}^2
\]
Vì đường thẳng chia hình thang thành hai phần bằng nhau ⇒ mỗi phần có diện tích:
\[
S_1 = S_2 = 30 \, \text{cm}^2
\]
Dựng phương trình cho diện tích phần trên
\[
\frac{(12 + d)}{2} \cdot x = 30 \quad \text{(1)}
\]
Tương tự, diện tích phần dưới:
\[
\frac{(d + 8)}{2} \cdot (6 - x) = 30 \quad \text{(2)}
\]
---
Giải hệ phương trình
Từ (1):
\[
(12 + d) \cdot x = 60 \quad \Rightarrow d = \frac{60}{x} - 12 \tag{3}
\]
Thay vào (2):
\[
\left( \frac{ \left( \frac{60}{x} -12 \right) + 8 }{2} \right) \cdot (6 - x) = 30
\Rightarrow \frac{ \left( \frac{60}{x} -4 \right)}{2} \cdot (6 - x) = 30
\]
Nhân 2 vế với 2 để khử mẫu:
\[
\left( \frac{60}{x} - 4 \right) \cdot (6 - x) = 60
\]
Nhân phá:
\[
\frac{60 \cdot (6 - x)}{x} - 4(6 - x) = 60
\]
Tính:
\[
\frac{360 - 60x}{x} - (24 - 4x) = 60
\Rightarrow \frac{360 - 60x}{x} = 60 + 24 - 4x = 84 - 4x
\]
Giải:
\[
\frac{360 - 60x}{x} = 84 - 4x
\Rightarrow 360 - 60x = x(84 - 4x)
\Rightarrow 360 - 60x = 84x - 4x^2
\Rightarrow -4x^2 + 144x - 360 = 0
\]
Chia cả phương trình cho 4:
\[
x^2 - 36x + 90 = 0
\]
Giải phương trình:
\[
x = \frac{36 \pm \sqrt{(-36)^2 - 4 \cdot 1 \cdot 90}}{2}
= \frac{36 \pm \sqrt{1296 - 360}}{2}
= \frac{36 \pm \sqrt{936}}{2}
\]
\[
\sqrt{936} \approx 30.6 \Rightarrow x \approx \frac{36 \pm 30.6}{2}
\Rightarrow x \approx \frac{5.4}{2} = 2.7 \, \text{hoặc} \, \frac{66.6}{2} = 33.3 \, (\text{loại})
\]
Đường thẳng đó cách đáy lớn khoảng 2,7 cm
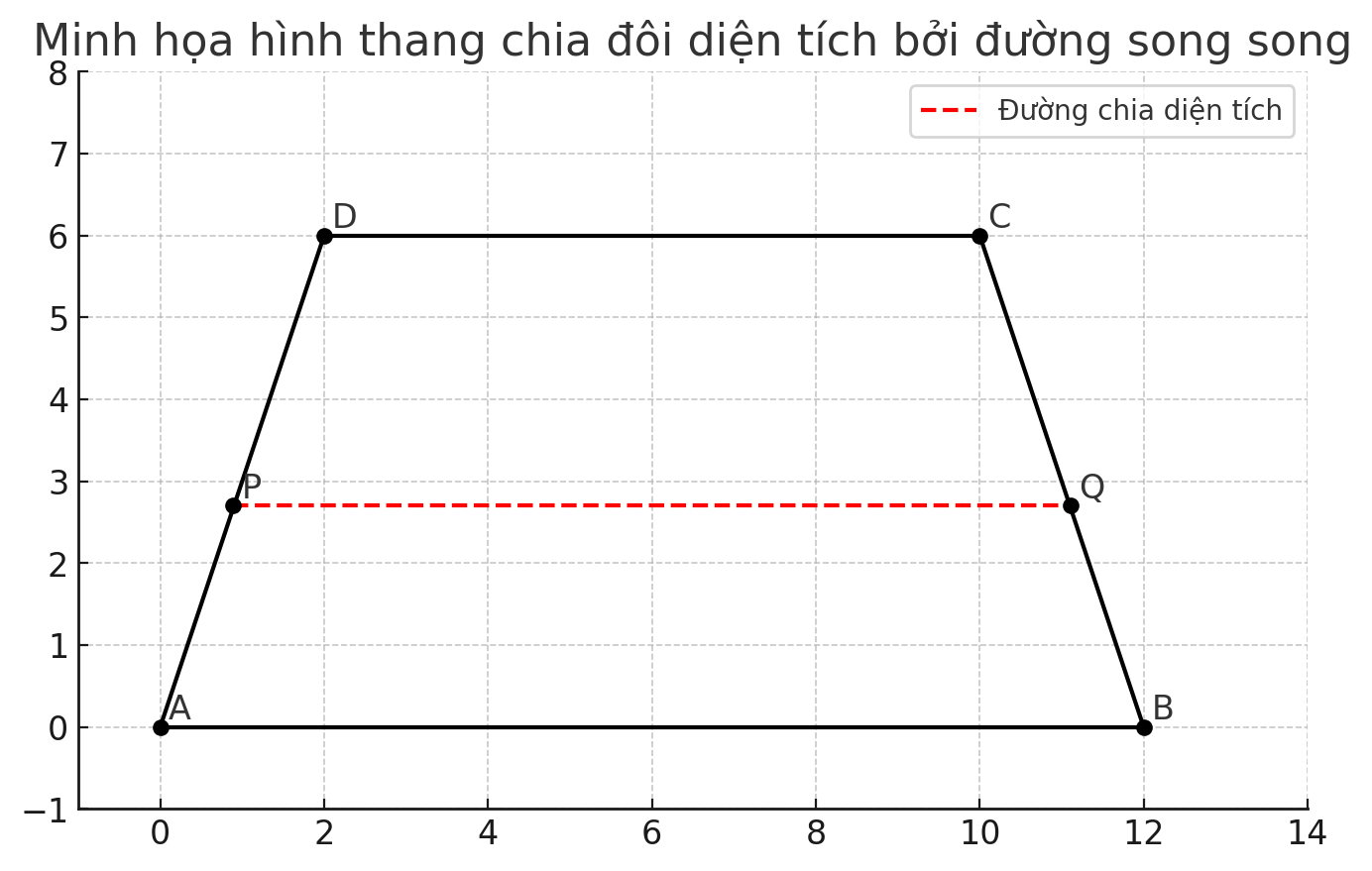
Gọi hình thang ban đầu là ABCD với AB là đáy lớn (12cm) và CD là đáy nhỏ (8cm), chiều cao 6cm. Gọi đường thẳng song song với hai đáy là MN.
1. Tính diện tích hình thang ABCD:
Diện tích hình thang ABCD là:
SABCD=2(AB+CD)×h=2(12+8)×6=60(cm2)
2. Tính diện tích mỗi hình thang nhỏ:
Vì đường thẳng MN chia hình thang ABCD thành hai hình thang nhỏ có diện tích bằng nhau, nên diện tích mỗi hình thang nhỏ là:
SAMND=SMBCN=2SABCD=260=30(cm2)
3. Tính độ dài đáy MN:
Gọi độ dài đáy MN là x (cm).
Gọi chiều cao của hình thang AMND là h1 (cm) và chiều cao của hình thang MBCN là h2 (cm). Ta có h1 + h2 = 6cm.
Diện tích hình thang AMND là:
SAMND=2(AB+MN)×h1=2(12+x)×h1=30
Diện tích hình thang MBCN là:
SMBCN=2(MN+CD)×h2=2(x+8)×h2=30
Ta có công thức tính độ dài đoạn thẳng song song với hai đáy của hình thang và chia hình thang đó thành hai hình thang có diện tích bằng nhau:
MN=2AB2+CD2=2122+82=2144+64=104=226(cm)
4. Tính chiều cao h1:
Thay MN = 226 vào công thức diện tích hình thang AMND:
30=2(12+226)×h1
h1=12+22660=6+2630=(6+26)(6−26)30(6−26)=36−2630(6−26)=3(6−26)(cm)
5. Tính khoảng cách từ MN đến đáy lớn AB:
Khoảng cách từ MN đến đáy lớn AB chính là chiều cao h1 của hình thang AMND. Vậy khoảng cách cần tìm là 3(6−26) cm.
Dữ kiện đề bài:
Đáy lớn: a=12 cma = 12 \, cma=12cm
Đáy bé: b=8 cmb = 8 \, cmb=8cm
Chiều cao: h=6 cmh = 6 \, cmh=6cm
Một đường thẳng song song với hai đáy, chia hình thang thành hai hình thang có diện tích bằng nhau.
Bước 1: Tính diện tích toàn bộ hình thang
S=12(a+b)⋅h=12(12+8)⋅6=12⋅20⋅6=60 cm2S = \frac{1}{2}(a + b) \cdot h = \frac{1}{2}(12 + 8) \cdot 6 = \frac{1}{2} \cdot 20 \cdot 6 = 60 \, cm^2S=21(a+b)⋅h=21(12+8)⋅6=21⋅20⋅6=60cm2Vì chia đôi diện tích:
⇒Mo^~ihıˋnhthangnhỏcoˊdiệntıˊch:602=30 cm2\Rightarrow Mỗi hình thang nhỏ có diện tích: \frac{60}{2} = 30 \, cm^2⇒Mo^~ihıˋnhthangnhỏcoˊdiệntıˊch:260=30cm2
Bước 2: Gọi độ dài đáy trung gian cần tìm là xxx (đường thẳng chia hình), và khoảng cách từ đáy lớn đến đường thẳng đó là h1h_1h1
Khi đó:
Hình thang dưới có hai đáy: 12 cm12 \, cm12cm và x cmx \, cmxcm, chiều cao: h1h_1h1
Diện tích hình thang dưới:
S1=12(12+x)⋅h1=30S_1 = \frac{1}{2}(12 + x) \cdot h_1 = 30S1=21(12+x)⋅h1=30➡️ Giải phương trình:
(12+x)⋅h1=60(1)(12 + x) \cdot h_1 = 60 \quad \text{(1)}(12+x)⋅h1=60(1)Vì tổng chiều cao là 6 cm, nên hình thang trên có chiều cao là:
h2=6−h1h_2 = 6 - h_1h2=6−h1Hình thang trên có đáy: xxx và 888, diện tích cũng là 30 cm²:
12(x+8)(6−h1)=30⇒(x+8)(6−h1)=60(2)\frac{1}{2}(x + 8)(6 - h_1) = 30 \Rightarrow (x + 8)(6 - h_1) = 60 \quad \text{(2)}21(x+8)(6−h1)=30⇒(x+8)(6−h1)=60(2)
Bước 3: Giải hệ phương trình
Từ (1):
h1=6012+xh_1 = \frac{60}{12 + x}h1=12+x60Thế vào (2):
(x+8)(6−6012+x)=60(x + 8) \left(6 - \frac{60}{12 + x} \right) = 60(x+8)(6−12+x60)=60Giải:
(x+8)((6)(12+x)−6012+x)=60⇒(x+8)⋅(72+6x−6012+x)=60⇒(x+8)⋅(12+6x12+x)=60(x + 8) \left( \frac{(6)(12 + x) - 60}{12 + x} \right) = 60 \Rightarrow (x + 8) \cdot \left( \frac{72 + 6x - 60}{12 + x} \right) = 60 \Rightarrow (x + 8) \cdot \left( \frac{12 + 6x}{12 + x} \right) = 60(x+8)(12+x(6)(12+x)−60)=60⇒(x+8)⋅(12+x72+6x−60)=60⇒(x+8)⋅(12+x12+6x)=60Nhân hai vế:
(x+8)(6x+12)x+12=60\frac{(x + 8)(6x + 12)}{x + 12} = 60x+12(x+8)(6x+12)=60Rút gọn:
(x+8)(6x+12)x+12=60⇒(x+8)(6x+12)=60(x+12)\frac{(x + 8)(6x + 12)}{x + 12} = 60 \Rightarrow (x + 8)(6x + 12) = 60(x + 12)x+12(x+8)(6x+12)=60⇒(x+8)(6x+12)=60(x+12)Nhân vế trái:
(x+8)(6x+12)=6x2+12x+48x+96=6x2+60x+96(x + 8)(6x + 12) = 6x^2 + 12x + 48x + 96 = 6x^2 + 60x + 96(x+8)(6x+12)=6x2+12x+48x+96=6x2+60x+96Vế phải:
60x+72060x + 72060x+720Lập phương trình:
6x2+60x+96=60x+720⇒6x2=624⇒x2=104⇒x=104≈10.2 (cm)6x^2 + 60x + 96 = 60x + 720 \Rightarrow 6x^2 = 624 \Rightarrow x^2 = 104 \Rightarrow x = \sqrt{104} \approx 10.2 \, (cm)6x2+60x+96=60x+720⇒6x2=624⇒x2=104⇒x=104≈10.2(cm)
Bước 4: Tìm khoảng cách từ đáy lớn đến đường chia (chiều cao hình thang dưới)
Từ (1):
h1=6012+x=6012+104≈6012+10.2≈6022.2≈2.7 cmh_1 = \frac{60}{12 + x} = \frac{60}{12 + \sqrt{104}} \approx \frac{60}{12 + 10.2} \approx \frac{60}{22.2} \approx 2.7 \, cmh1=12+x60=12+10460≈12+10.260≈22.260≈2.7cm
✅ Vậy đường thẳng đó cách đáy lớn khoảng 2,7 cm\boxed{2{,}7 \, \text{cm}}2,7cm
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
5117
Đã trả lời bởi chuyên gia
5117 -
 Đã trả lời bởi chuyên gia
4339
Đã trả lời bởi chuyên gia
4339