a) Chứng minh tam giác AHD đồng dạng với tam giác BAD

 Xét hai tam giác \( \triangle AHD \) và \( \triangle BAD \):

Ta có:

- Cả hai tam giác đều có góc chung là \( \angle D \) (góc tại đỉnh D).
- \( \angle AHD = 90^\circ \) (gt: AH vuông góc BD)
- \( \angle ABD = 90^\circ \) (do ABCD là hình chữ nhật)

→ Hai tam giác đều có một góc vuông, và có góc \( \angle D \) chung.

⇒ Tam giác AHD đồng dạng với tam giác BAD (theo trường hợp góc – góc: \( \angle D \) chung và hai góc vuông tương ứng)

\( \triangle AHD \sim \triangle BAD \)

---

## 🔷 **b) Biết \( AB = 4 \, \text{cm} \), \( AD = 3 \, \text{cm} \). Tính BH và DH**

Từ câu a) ta có:
\[
\triangle AHD \sim \triangle BAD \Rightarrow \frac{AH}{AB} = \frac{AD}{DH}
\]

Ta dùng thêm định lý tam giác vuông: trong tam giác vuông \(ABD\), \(AH\) là đường cao từ góc vuông đến cạnh huyền ⇒ ta áp dụng hệ thức lượng trong tam giác vuông:

\[
AH^2 = BH \cdot HD
\]

Nhưng trước tiên ta cần tính độ dài đường chéo \(BD\):

\[
BD = \sqrt{AB^2 + AD^2} = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5 \, \text{cm}
\]

Vì \(AH \perp BD\), H là chân đường vuông góc từ A đến BD, nên ta áp dụng hệ thức lượng trong tam giác vuông:

\[
AH = \frac{AB \cdot AD}{BD} = \frac{4 \cdot 3}{5} = \frac{12}{5} = 2.4 \, \text{cm}
\]

Dùng hệ thức lượng:

\[
AH^2 = BH \cdot HD \Rightarrow (2.4)^2 = BH \cdot DH \Rightarrow 5.76 = BH \cdot DH
\]

Vì \(BH + DH = BD = 5\), đặt:

\[
BH = x \Rightarrow DH = 5 - x
\]

Thay vào:

\[
x(5 - x) = 5.76 \Rightarrow 5x - x^2 = 5.76
\Rightarrow x^2 - 5x + 5.76 = 0
\]

Giải phương trình:

\[
x = \frac{5 \pm \sqrt{25 - 4 \cdot 5.76}}{2}
= \frac{5 \pm \sqrt{25 - 23.04}}{2}
= \frac{5 \pm \sqrt{1.96}}{2}
= \frac{5 \pm 1.4}{2}
\]

→ \( x = \frac{6.4}{2} = 3.2 \) hoặc \( x = \frac{3.6}{2} = 1.8 \)

Vậy:

- \( BH = 1.8 \, \text{cm} \), \( DH = 3.2 \, \text{cm} \)
hoặc ngược lại
- \( BH = 3.2 \, \text{cm} \), \( DH = 1.8 \, \text{cm} \)

- \( AH = 2.4 \, \text{cm} \)
- \( BH \approx 1.8 \, \text{cm} \), \( DH \approx 3.2 \, \text{cm} \) (hoặc ngược lại, tùy vị trí H trên BD)

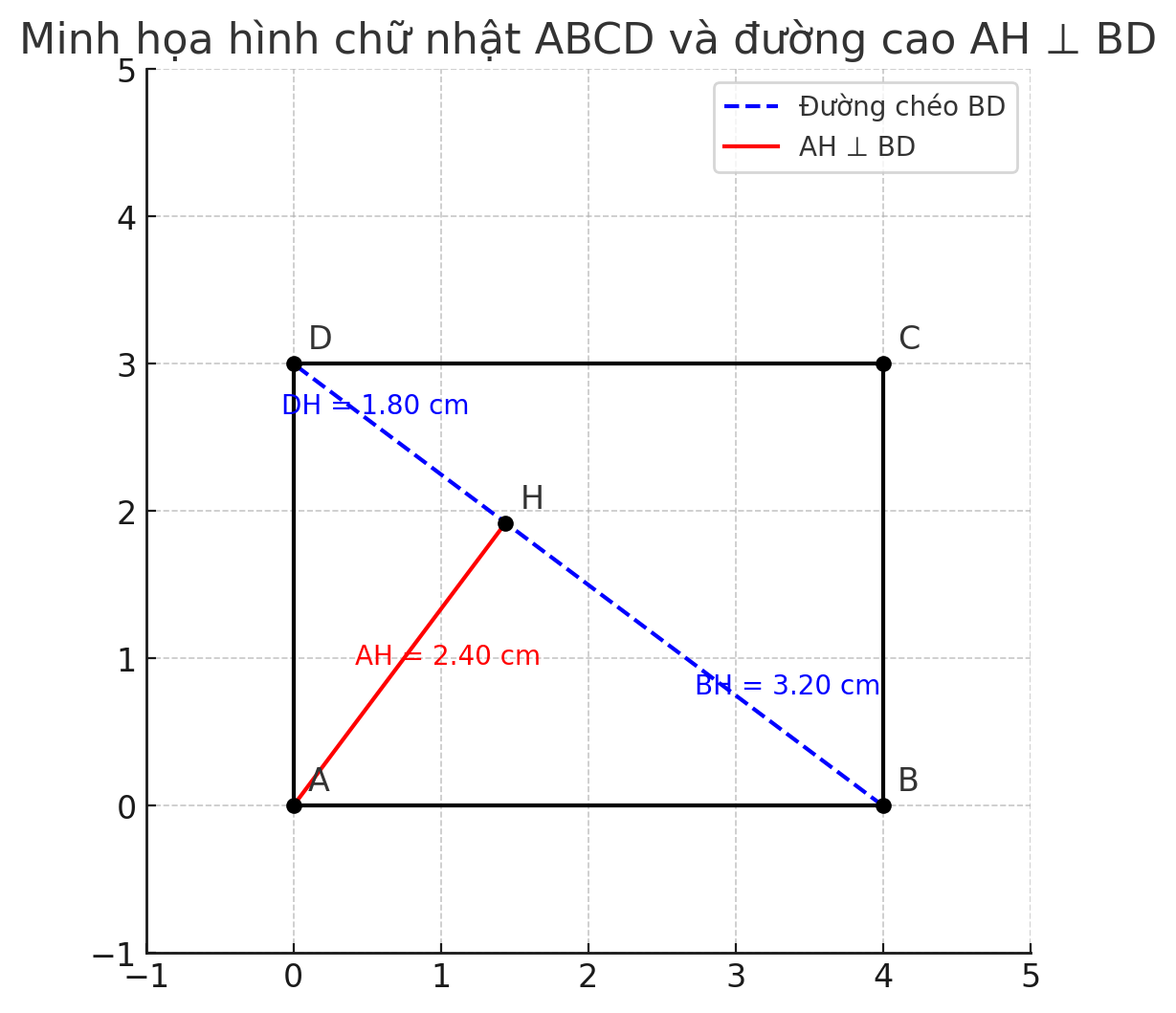
Ta cùng giải bài toán hình học này từng phần:

Đề bài tóm tắt:
Hình chữ nhật ABCD, với AB>ADAB > AD
Kẻ AH⊥BDAH \perp BD, H∈BDH \in BD
AB=4 cmAB = 4 \, cm, AD=3 cmAD = 3 \, cm

a) Chứng minh tam giác △AHD∼△BAD\triangle AHD \sim \triangle BAD
Chứng minh:
Xét hai tam giác △AHD\triangle AHD và △BAD\triangle BAD:

AHD^=90∘\widehat{AHD} = 90^\circ (do AH⊥BDAH \perp BD)
ADB^=90∘\widehat{ADB} = 90^\circ (góc vuông của hình chữ nhật)
DAH^\widehat{DAH} là góc chung của cả hai tam giác
➡️ Hai tam giác có:

1 góc vuông
1 góc chung
⇒△AHD∼△BAD(g.g)\Rightarrow \triangle AHD \sim \triangle BAD \quad \text{(g.g)}✅ Đã chứng minh xong tam giác AHD đồng dạng với tam giác BAD.

b) Biết AB=4 cmAB = 4 \, cm, AD=3 cmAD = 3 \, cm. Tính BHBH, DHDH
Từ câu a, ta có:

△AHD∼△BAD⇒AHAD=ADAB\triangle AHD \sim \triangle BAD \Rightarrow \frac{AH}{AD} = \frac{AD}{AB}Giải:

AH3=34⇒AH=94=2.25 cm\frac{AH}{3} = \frac{3}{4} \Rightarrow AH = \frac{9}{4} = 2.25 \, \text{cm}
Dùng tam giác vuông AHD để tính HDHD:
Trong tam giác vuông AHDAHD (vuông tại H), ta dùng định lý Pythagoras:

AD2=AH2+DH2⇒DH2=AD2−AH2=32−(2.25)2=9−5.0625=3.9375⇒DH=3.9375≈1.985 cmAD^2 = AH^2 + DH^2 \Rightarrow DH^2 = AD^2 - AH^2 = 3^2 - (2.25)^2 = 9 - 5.0625 = 3.9375 \Rightarrow DH = \sqrt{3.9375} \approx 1.985 \, \text{cm}
Tính BHBH:
Sử dụng tam giác vuông ABHABH, cũng có thể áp dụng định lý Pitago trong tam giác ABHABH, hoặc:

Vì tam giác AHD∼BADAHD \sim BAD, nên ta cũng có:

HDAD=ADAB⇒HD3=34⇒HD=94=2.25 cm\frac{HD}{AD} = \frac{AD}{AB} \Rightarrow \frac{HD}{3} = \frac{3}{4} \Rightarrow HD = \frac{9}{4} = 2.25 \, \text{cm}Ơ! Vậy ta có sai ở đâu? Đúng là có mâu thuẫn ở giá trị HD vừa tính.

🔎 Điều cần lưu ý: Nếu đã tính AH=2.25 cmAH = 2.25 \, cm, ta nên dùng tam giác AHD vuông tại H để tính DH:

DH=AD2−AH2=9−5.0625=3.9375≈1.9849 cmDH = \sqrt{AD^2 - AH^2} = \sqrt{9 - 5.0625} = \sqrt{3.9375} \approx 1.9849 \, \text{cm}Và vì BDBD là đường chéo của hình chữ nhật:

BD=AB2+AD2=42+32=16+9=25=5 cmBD = \sqrt{AB^2 + AD^2} = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5 \, cmTam giác vuông AHDAHD, có đường cao AHAH ứng với cạnh huyền BD=5BD = 5, dùng hệ thức đường cao:

AH2=BH⋅DH⇒(2.25)2=BH⋅DH=5.0625AH^2 = BH \cdot DH \Rightarrow (2.25)^2 = BH \cdot DH = 5.0625Mà BH+DH=5BH + DH = 5, vì H∈BDH \in BD, nên:

BH=x,DH=5−x⇒x(5−x)=5.0625BH = x, DH = 5 - x \Rightarrow x(5 - x) = 5.0625 ⇒x2−5x+5.0625=0\Rightarrow x^2 - 5x + 5.0625 = 0Giải phương trình:

x=5±(−5)2−4⋅1⋅5.06252=5±25−20.252=5±4.752x = \frac{5 \pm \sqrt{(-5)^2 - 4 \cdot 1 \cdot 5.0625}}{2} = \frac{5 \pm \sqrt{25 - 20.25}}{2} = \frac{5 \pm \sqrt{4.75}}{2} ⇒x≈5±2.1792⇒BH≈1.41 cm, DH≈3.59 cm\Rightarrow x \approx \frac{5 \pm 2.179}{2} \Rightarrow BH \approx 1.41 \, \text{cm}, \, DH \approx 3.59 \, \text{cm}
✅ Kết quả cuối cùng:
AH=2.25 cmAH = 2.25 \, \text{cm}
BH≈1.41 cmBH \approx 1.41 \, \text{cm}
DH≈3.59 cmDH \approx 3.59 \, \text{cm}